1. INTRODUCTION
The wood construction market has been growing each year, and the number of wood construction projects permitted in 2017 reached about 17,000 (Ministry of Land, Infrastructure and Transport, 2017). Corresponding to about twice as many as the number of permitted masonry constructions, wood constructions occupy a considerable ratio in the construction market. Many wood constructions use light-frame wood constructions, which use structures with relatively small structural elements like beams, studs, and underflooring inside walls or floor covers. Accordingly, the performance of dimensional lumber is very important.
Despite the consistent growth of the wood construction market, domestic lumbers in South Korea are rarely used as structural purposes. Instead, lumbers imported from North America, New Zealand, or Japan are used in light-frame wood constructions. It is believed this is due to the priority of the reforestation policy, rather than the use of forest, leading to the negligence in the use of domestic lumbers. However, such a situation is changing with the increase in the needs for the application of rich resources thanks to the reforestation policy and the Korean government's adoption of the Paris Agreement, which was based on the UNFCCC. Thus, the increased use of domestic lumbers is expected as a high value-added material that will help continue the carbon fixation effect of lumber.
The use of domestic lumber as structural materials requires accurate design values. For not only will these values guarantee structural stability of constructions, but they will be essential in sufficiently producing engineering lumber. Such values are determined by standard testing methods. Particularly, since lumber has its unique defects, there is a large deviation of properties, which is affected by testing conditions, and thus, the standard testing method is important.
There has been active research in the change of the mechanical properties of lumber based on testing methods. Gerhards and Link (1986) examined the effect of loading speed on the bending strength of lumber, reporting that the average bending strength of lumber increased almost linearly to the log of the loading speed. Schneeweiß and Felber (2013) conducted a bending test on oak and Korean spruce under the four-point loading test and the central loading test, confirming that the bending strength under the central loading test was lower than that under the four-point loading test. Bechtel and Norris (1959) reported that the bending strength of non-defect small specimen Sitka suruce increased by the increase of the span length-depth ratio. Isaksson (1999) studied the load support performance and span length of beams for structural lumber, showing that the increase in the span length would reduce the load support performance of beams.
The lumber bending test method in South Korea is defined by KS F 2150, the method of static bending test for full sized structural lumber by the Korean Industrial Standards (KS). The testing conditions for KS F 2150 are mostly similar to those of foreign standards, but there is a difference in the span length-depth ratio. Considering that KS F 2150 proposes that over 15 of the span length-depth ratio, span length can be freely set, there may be some questions with regard to the aforementioned research results. Thus, this study examined the effect of the span length-depth ratio on the bending properties of visually graded Korean pine lumber.
2. MATERIALS and METHODS
The test used Korean pine (Lartix kaempferi (Lamb.) Carriere), which is abundant in Korea and is preferred as structural use, as the specimen. Kiln dried 2 × 4 Korean pine lumber (38 (width) × 89 (depth) × 3,600 (length) mm3) was purchased from the Jungbu Lumber Distribution Center (Yeoju, Gyeonggi) at National Forestry Cooperatives Federation. The number of the purchased lumbers was 550, and 248 visually graded No. 1 specimens were used in the test. The visual grading was performed by the dimension and quality standard for lumber products by the National Institute of Forest Science, which is shown in Table 1. Visually graded No. 1 Korean pine lumber was stored in a constant temperature and humidity room (20°C, relative humidity 65%) so as to have it reach the equilibrium moisture content. The average moisture content of the specimens was 10.5±1.5%, and the average air-dry density was 543.5±62.3 kg/m3.
The study conducted the four-point bending test using a universal material testing machine (MTS, U.S.), aiming to examine the impact of span length on the bending performance using two types of span length (1,650 and 3,000 mm). Here, the span length-depth ratio was 18.5 and 33.7 at the span length of 1,650 mm and 3,000 mm, respectively. According to the method of static bending test by KS (KS F 2150), the test speed was set so that the failure would occur at about 6 minutes on the average in the bending test at each condition. While the bending test is in progress, the rotary variable differential transformer (Kyowa, Japan) was used to measure the displacement of the central axis between the span length. Using the measured load and displacement values, the study acquired the modulus of elasticity, including the bending strength and shear deformation of the narrow dimensional section. The defects affecting the grade were placed arbitrarily between the load span length regardless of the tensile and compressive sections. Shown in Fig. 1 is the diagram of the bending test.
To verify if the bending performance changes by span length, t-test was conducted on the bending strength and the modulus of elasticity at 5% of significance level. Before starting the t-test, F-test was conducted at 5% of significance level for verifying the significance difference in bending performance based on each span length. While the modulus of elasticity uses the average value as the representative value, the bending strength uses the standard allowable stress based on the 5% of the lower limit as the representative value. Thus, to determine the change of the bending strength by span length, the bending standard allowable stress by condition was determined and compared. To determine the standard allowable stress, 5% lower limit was calculated by the normal, lognormal, and 2-parameter Weibull distributions as the parametric methods. The probability density function of each distribution can be defined in the following.
- Normal distribution
- Lognormal distribution
- Weibull distribution
Here, e = Euler's constant, ln = natural log, μ= average, σ= standard deviation,
3. RESULTS and DISCUSSION
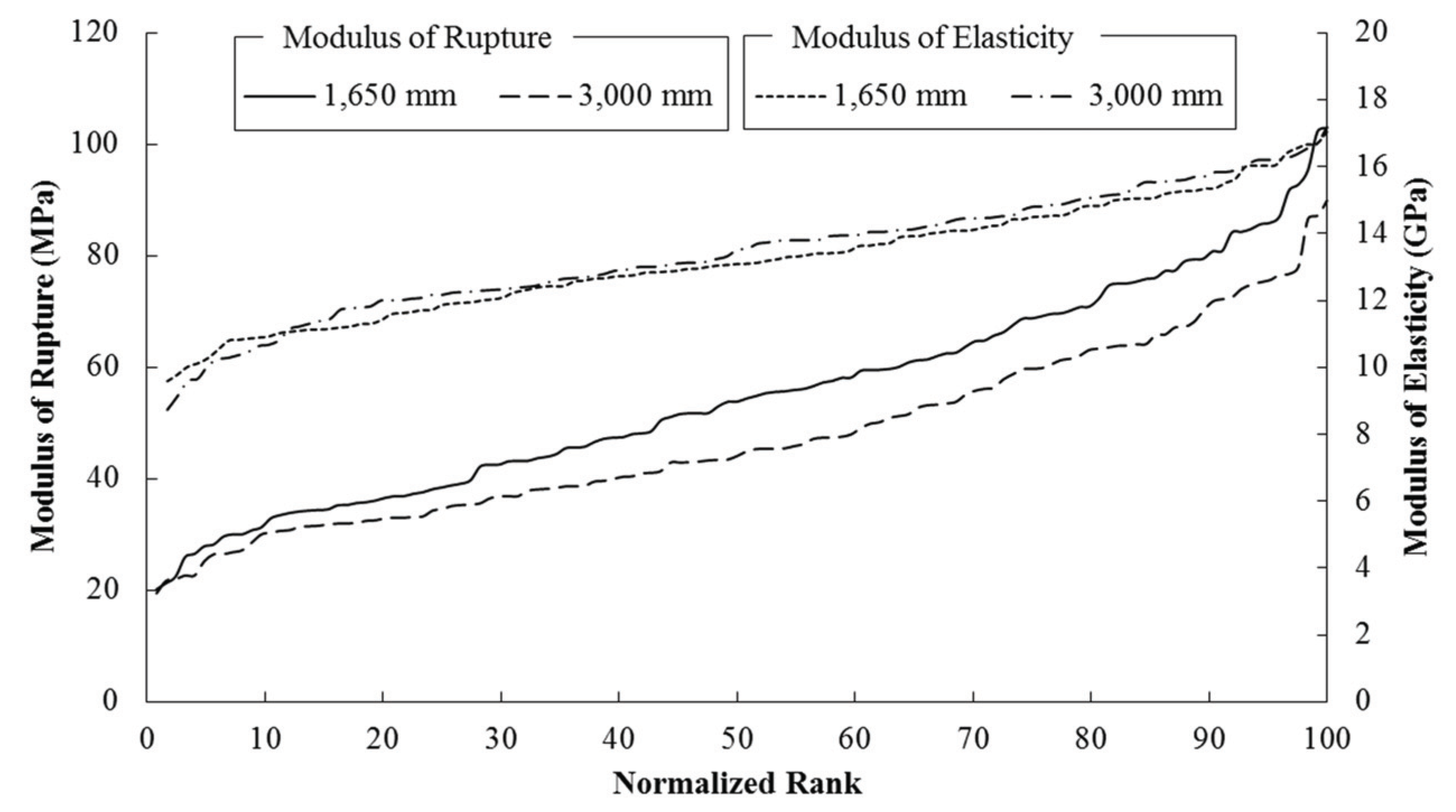
To examine the bending strength change of visually graded No. 1 lumber by span length, the bending strength was calculated by using the maximum load acquired from the bending test. Shown in Table 2 are the statistical results of the bending strength by span length. In F test, p value was 0.070, higher than the significance level at 5%, showing that the difference in bending strength between distributions by span length was statistically insignificant. Thus, assuming the equal variance, t test was conducted on the results of the average bending strength based on the two conditions. The result showed that p value was 0.001, lower than the significance level at 5%, and thus, the null hypothesis was rejected. In other words, it could be concluded that there would exist a difference between the average bending strength values by span length. The average bending strength under the span length of 1,650 mm was 55.01 MPa, which was considerably larger than that under the span length of 3,000 mm, which was 47.54 MPa (Table 2).
Shown in Table 3 are the fitness distribution test results on the bending strength, which was conducted to determine the standard allowable stress change of visually graded No. 1 lumber by span length. The chi-square test at 5% of significance level showed that at the span length of 1,650 mm, the result followed the normal, lognormal, and Weibull distributions whereas at the span length of 3,000 mm, only the lognormal distribution was fit. Since the 5% lower limit of bending strength can differ by the fitness distribution, it was calculated by using the lognormal distribution determined to be fit commonly in both span lengths. At 1,650 mm, 5% lower limit was 28.65 MPa whereas at 3,000 mm, it was 25.70 MPa so that, like the average bending strength, the longer the span length, the lower the 5% lower limit became. The difference between the average bending strength and the 5% lower limit of bending strength based on span length was 7.44 MPa and 2.95 MPa, respectively, showing that, as in Fig. 2, the increase in the percentage led to the increase in the difference.
The study compared the bending standard allowable stress calculated by multiplying 0.475 to the 5% lower limit of the bending strength based on span length and the design allowable stress, which was produced by multiplying the size coefficient 1.5, proposed by KS F 2162, to the standard allowable stress of the grade No. 1 larch, proposed by the dimension and quality standards of lumber by the National Institute of Forest Science. The standard allowable stress at 1,650 mm and 3,000 mm was 13.61 MPa and 12.21 MPa, respectively; conversely, the design allowable stress of No. 1 grade larch was 11.7 MPa, lower than the standard allowable stress by span length (Table 4). It is believed that this is because the standard allowable stress proposed by the lumber dimension and quality standards of the National Institute of Forest Science was derived from clear wood specimens. Kong and Jeong (2015) reported that since the strength reduction ratio by grade applied to the allowable stress calculation for non-defect small specimens was set high, resulting in a value lower than the allowable stress value by lumber grade.
| Span length (mm) | Test result (MPa) | Allowable stress in standard1)(MPa) | ||
|---|---|---|---|---|
| 5th percentile | Allowable stress | No. 1 | Size-adjusted value | |
| 1,650 | 28.65 | 13.61 | 7.8 | 11.7 |
| 3,000 | 25.70 | 12.21 | ||
On the contrary, as shown in Table 2 and Fig. 2, the average modulus of elasticity of visually graded No. 1 larch lumber, tends to increase as the span length increases, but there was no significant difference by span length. Madsen (1992) studied the change of the modulus of elasticity by four different span lengthto- depth ratios (12, 18.3, 25.7, and 38.6) in the bending test of a 38×89 mm lumber specimen, the result of which verified the result of this study, that is, the increase in the span length increased the modulus of the average bending elasticity. Here, the same tendency was reported despite that the removal of the effect of the shear deformation changed the modulus of elasticity. While no clear reason for the change of the modulus of the elasticity by span length was given, Barrett et al. (1994) reported that when the span length-depth ratio was small and the ratio of the modulus of elasticity to the modulus of stiffness, including shear deformation, was large, the span length-depth ratio made a huge effect on the modulus of elasticity including shear deformation. However, it was also reported that the ratio of the modulus of elasticity and the modulus of stiffness including shear deformation would change, and therefore, it is believed that additional research would be necessary on the change of the modulus of elasticity by span length on the bending lumber.
It was shown that in bending performance, the span length changed bending strength more than the modulus of elasticity. Such a result can be explained by the weakest link failure theory (Weibull, 1993), which was developed under the assumption that the natural change of the strength properties in lumber is arbitrary and is not related to each other. In a zone under high stress, the probability that weaker areas are to be included would increase as the size of materials increases, and therefore, the strength decreases in inversion to the increase in the size of the material. As such, the phenomenon where the properties of a material change by the size of the material is called size effect, which is known to increase in the strength that shows brittle failure mode due to defects or weak parts in the material rather than in the modulus of elasticity, which has the concept of the mean average (Hwang et al., 2003). As such, the span length changed bending strength more drastically in the bending performance.
To consider the size effect in lumber, ASTM D1990 proposes an equation that converts the strength data acquired by the test to a specific size. For the bending strength, the equation in ASTM D1990 uses 0.14 as the modulus of size in length. Barrett et al. (1995) reported that in the visually graded Hem-Fir and S-P-F, the modulus of size in length was 0.18 and 0.16, respectively. Within the 5% lower limit of bending strength, acquired by the test of this study, the modulus of size in length, acquired by the regressive analysis of the log value in strength and the log value in length (Barrett et al., 1995) was 0.18, showing that as in Fig. 3, larch had a large size effect when compared to ASTM D1990.
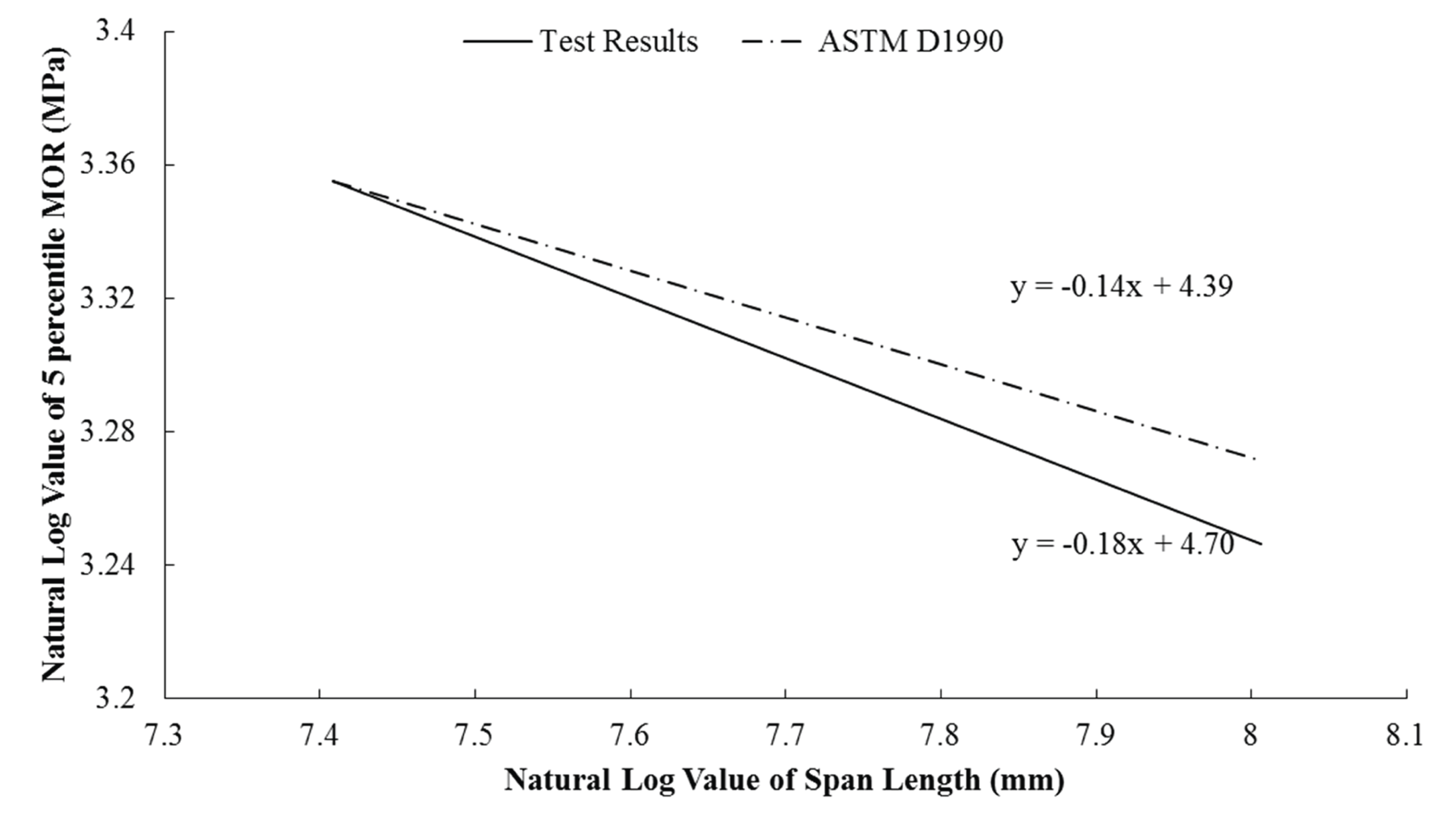
While there has been consistent research on the bending test for lumber in South Korea (Park et al., 2010; Pang et al., 2013), Oh (2014), which compared the value from literature to the modulus of size in length through the regression analysis of the log value in strength and the log value in depth in bending strength, is the only research on size effect. Thus, it is determined that additional research on size effect is necessary. Particularly, it is believed that it is possible to include an equation that can consider size effect as in ASTM D1990 or to make revisions in which to include an equation to consider size effect as well as limiting the span length-to-depth ratio in KS F 2150. Considering that the length of generally used lumber is 3,600 mm, various types of span length can be selected based on the cross-section of the produced lumber, and therefore, it is expected that the problem of different results of bending tests even by following the KS standards could be compensated. Furthermore, the strength values acquired from lumber in various sizes can be reflected to the design values.
4. CONCLUSION
The study conducted a bending test on 38 × 89 mm lumber to determine the effect of span length on the bending performance of structural lumber. The result showed a significant change of bending strength among the bending performance properties by span length within 5% of significance level. The 5% lower limit of the bending strength increased as the span length shortened, as in 28.65 MPa at 1,650 mm, and 25.70 MPa at 3,000 mm. It is believed that this was due to size effect, and it is determined that a corresponding compensation method of strength values by size would need to be included in KS F 2150. It is expected that in this way, various strength values from different sizes of lumber can be reflected to design values.

