Change of Bending Properties of 2×4 Larch Lumber According to Span Length in the Four Point Bending Test

Kim, Chul-Ki; Kim, Kwang-Mo; Lee, Sang-Joon; Park, Moon-Jae

doi:10.5658/WOOD.2018.46.5.486

2018; 46(5):486-496

pISSN: 1017-0715, eISSN: 2233-7180

DOI: https://doi.org/10.5658/WOOD.2018.46.5.486

Original Article

Change of Bending Properties of 2×4 Larch Lumber According to Span Length in the Four Point Bending Test

Chul-Ki Kim², Kwang-Mo Kim², Sang-Joon Lee², Moon-Jae Park²^,^†

Author Information & Copyright ▼

²Wood Engineering Division, Forest Products Department, National Institute of Forest Science, 57 Heogi-ro, Dongdaemun-gu, Seoul, 02455, Republic of Korea

^†Corresponding author: Moon-Jae Park (e-mail: mjpark@korea.kr, ORCID: 0000-0001-8948-327X)

Received: Jul 26, 2018; Accepted: Sep 03, 2018

Published Online: Sep 25, 2018

Abstract

This study was conducted to confirm an effect of span length on bending properties of larch dimensional lumber in the four point bending test. The size of specimen in this study was 38 (width) × 89 (depth) × 3,600 (length) mm³, and average air-dry density and moisture content of the specimens was 543.5 kg/m³ and 10.5%, respectively. Visually graded No. 1 dimensional lumbers of 248 were divided by two groups to compare modulus of rupture (MOR) and modulus of elasticity (MOE). One group was tested in the four point bending test with span length of 1,650 mm, and other was tested with span length of 3,000 mm. While MOE was not different according to span length in 5% significance level, MOR was different in accordance with span lengths and was in inverse proportion to change of span length. Fifth percentiles of MOR in span length of 1,650 and 3,000 mm were 28.65 and 25.70 MPa, respectively. It was confirmed that the difference between MORs in each case increased as normalized rank increased. This is because of size effect in Weibull weakest link failure theory. Therefore, KS F 2150, in which there is only regulation about span to depth ratio of 15 or more, is needed to be revised to contain a method considering size effect for MOR. From the method, various results of bending test with different size of lumber could be used to determine design value of lumber.

Keywords: dimensional lumber; bending property; modulus of rupture; modulus of elasticity; span length; the four point bending test; size effect

1. INTRODUCTION

The wood construction market has been growing each year, and the number of wood construction projects permitted in 2017 reached about 17,000 (Ministry of Land, Infrastructure and Transport, 2017). Corresponding to about twice as many as the number of permitted masonry constructions, wood constructions occupy a considerable ratio in the construction market. Many wood constructions use light-frame wood constructions, which use structures with relatively small structural elements like beams, studs, and underflooring inside walls or floor covers. Accordingly, the performance of dimensional lumber is very important.

Despite the consistent growth of the wood construction market, domestic lumbers in South Korea are rarely used as structural purposes. Instead, lumbers imported from North America, New Zealand, or Japan are used in light-frame wood constructions. It is believed this is due to the priority of the reforestation policy, rather than the use of forest, leading to the negligence in the use of domestic lumbers. However, such a situation is changing with the increase in the needs for the application of rich resources thanks to the reforestation policy and the Korean government's adoption of the Paris Agreement, which was based on the UNFCCC. Thus, the increased use of domestic lumbers is expected as a high value-added material that will help continue the carbon fixation effect of lumber.

The use of domestic lumber as structural materials requires accurate design values. For not only will these values guarantee structural stability of constructions, but they will be essential in sufficiently producing engineering lumber. Such values are determined by standard testing methods. Particularly, since lumber has its unique defects, there is a large deviation of properties, which is affected by testing conditions, and thus, the standard testing method is important.

There has been active research in the change of the mechanical properties of lumber based on testing methods. Gerhards and Link (1986) examined the effect of loading speed on the bending strength of lumber, reporting that the average bending strength of lumber increased almost linearly to the log of the loading speed. Schneeweiß and Felber (2013) conducted a bending test on oak and Korean spruce under the four-point loading test and the central loading test, confirming that the bending strength under the central loading test was lower than that under the four-point loading test. Bechtel and Norris (1959) reported that the bending strength of non-defect small specimen Sitka suruce increased by the increase of the span length-depth ratio. Isaksson (1999) studied the load support performance and span length of beams for structural lumber, showing that the increase in the span length would reduce the load support performance of beams.

The lumber bending test method in South Korea is defined by KS F 2150, the method of static bending test for full sized structural lumber by the Korean Industrial Standards (KS). The testing conditions for KS F 2150 are mostly similar to those of foreign standards, but there is a difference in the span length-depth ratio. Considering that KS F 2150 proposes that over 15 of the span length-depth ratio, span length can be freely set, there may be some questions with regard to the aforementioned research results. Thus, this study examined the effect of the span length-depth ratio on the bending properties of visually graded Korean pine lumber.

2. MATERIALS and METHODS

2.1. Material

The test used Korean pine (Lartix kaempferi (Lamb.) Carriere), which is abundant in Korea and is preferred as structural use, as the specimen. Kiln dried 2 × 4 Korean pine lumber (38 (width) × 89 (depth) × 3,600 (length) mm³) was purchased from the Jungbu Lumber Distribution Center (Yeoju, Gyeonggi) at National Forestry Cooperatives Federation. The number of the purchased lumbers was 550, and 248 visually graded No. 1 specimens were used in the test. The visual grading was performed by the dimension and quality standard for lumber products by the National Institute of Forest Science, which is shown in Table 1. Visually graded No. 1 Korean pine lumber was stored in a constant temperature and humidity room (20°C, relative humidity 65%) so as to have it reach the equilibrium moisture content. The average moisture content of the specimens was 10.5±1.5%, and the average air-dry density was 543.5±62.3 kg/m³.

Table 1. Defect sizes for visual grading for dimensional lumber (ratio to depth)

Defect Categories			No. 1	No. 2	No. 3
Knot	Narrow		≤ 25%	≤ 35%	≤ 45%
	Wide	Edge	≤ 25%	≤ 35%	≤ 45%
		Centre	≤ 30%	≤ 45%	≤ 60%
		Check			≤ 100%	≤ 150%	≤ 200%
	Annual ring width			≤ 6 mm	≤8 mm	Unlimited
Slope of grain			≤ 1/10	≤ 1/8	≤ 1/4

Download Excel Table

2.2. Bending test method

The study conducted the four-point bending test using a universal material testing machine (MTS, U.S.), aiming to examine the impact of span length on the bending performance using two types of span length (1,650 and 3,000 mm). Here, the span length-depth ratio was 18.5 and 33.7 at the span length of 1,650 mm and 3,000 mm, respectively. According to the method of static bending test by KS (KS F 2150), the test speed was set so that the failure would occur at about 6 minutes on the average in the bending test at each condition. While the bending test is in progress, the rotary variable differential transformer (Kyowa, Japan) was used to measure the displacement of the central axis between the span length. Using the measured load and displacement values, the study acquired the modulus of elasticity, including the bending strength and shear deformation of the narrow dimensional section. The defects affecting the grade were placed arbitrarily between the load span length regardless of the tensile and compressive sections. Shown in Fig. 1 is the diagram of the bending test.

Fig. 1. Schematic diagram of the four point bending test.

Download Original Figure

2.3. Statistical analysis

To verify if the bending performance changes by span length, t-test was conducted on the bending strength and the modulus of elasticity at 5% of significance level. Before starting the t-test, F-test was conducted at 5% of significance level for verifying the significance difference in bending performance based on each span length. While the modulus of elasticity uses the average value as the representative value, the bending strength uses the standard allowable stress based on the 5% of the lower limit as the representative value. Thus, to determine the change of the bending strength by span length, the bending standard allowable stress by condition was determined and compared. To determine the standard allowable stress, 5% lower limit was calculated by the normal, lognormal, and 2-parameter Weibull distributions as the parametric methods. The probability density function of each distribution can be defined in the following.

- Normal distribution

f x μ, σ 2 = 1 σ 2 π e − x − μ 2 / 2 σ 2

·············· (1)

- Lognormal distribution

f x m, v 2 = 1 x σ 2 π e − ln x − m 2 / 2 v 2

·············· (2)

- Weibull distribution

f x a, b = b a x a b − 1 e − x / a b

·············· (3)

Here, e = Euler's constant, ln = natural log, μ= average, σ= standard deviation, m=lnμ2/σ2+μ2,v=lnσ2/μ2+1, a = scale parameter, and b = shape parameter. Through the fitness test of the probability density function of each distribution, the 5% lower limit of the bending strength was calculated from the distribution that satisfies all the bending strength distribution properties based on the span length. The fitness test was conducted by the chi-square test at 5% of significance level. When calculating the standard allowable stress at the normal and lognormal distributions, 1.645 was used as k factor for the error limit (0.95) at 95% of confidence level. Later, as has been proposed by the decision method establishing allowable properties of softwood structural lumber (KS F 2152), the standard allowable stress was calculated by multiplying the 5% lower limit of the resulting bending strength to 0.475, the reduction factor determined by considering the normal loading period and safety coefficient.

3. RESULTS and DISCUSSION

To examine the bending strength change of visually graded No. 1 lumber by span length, the bending strength was calculated by using the maximum load acquired from the bending test. Shown in Table 2 are the statistical results of the bending strength by span length. In F test, p value was 0.070, higher than the significance level at 5%, showing that the difference in bending strength between distributions by span length was statistically insignificant. Thus, assuming the equal variance, t test was conducted on the results of the average bending strength based on the two conditions. The result showed that p value was 0.001, lower than the significance level at 5%, and thus, the null hypothesis was rejected. In other words, it could be concluded that there would exist a difference between the average bending strength values by span length. The average bending strength under the span length of 1,650 mm was 55.01 MPa, which was considerably larger than that under the span length of 3,000 mm, which was 47.54 MPa (Table 2).

Table 2. Statistics results of bending properties with two different span lengths

	Modulus of Rupture		Modulus of Elasticity
Span length (mm)	1,650	3,000	1,650	3,000
Aver. (MPa)	55.01	47.54	13,663	13,774
C. V.1)	0.34	0.34	0.18	0.15
Degree of freedom	123	123	123	123
Significant level	0.05		0.05
P value for Ftest	0.070		0.069
P value for ttest	0.001		0.813

¹⁾ C. V. is coefficient of variation

Download Excel Table

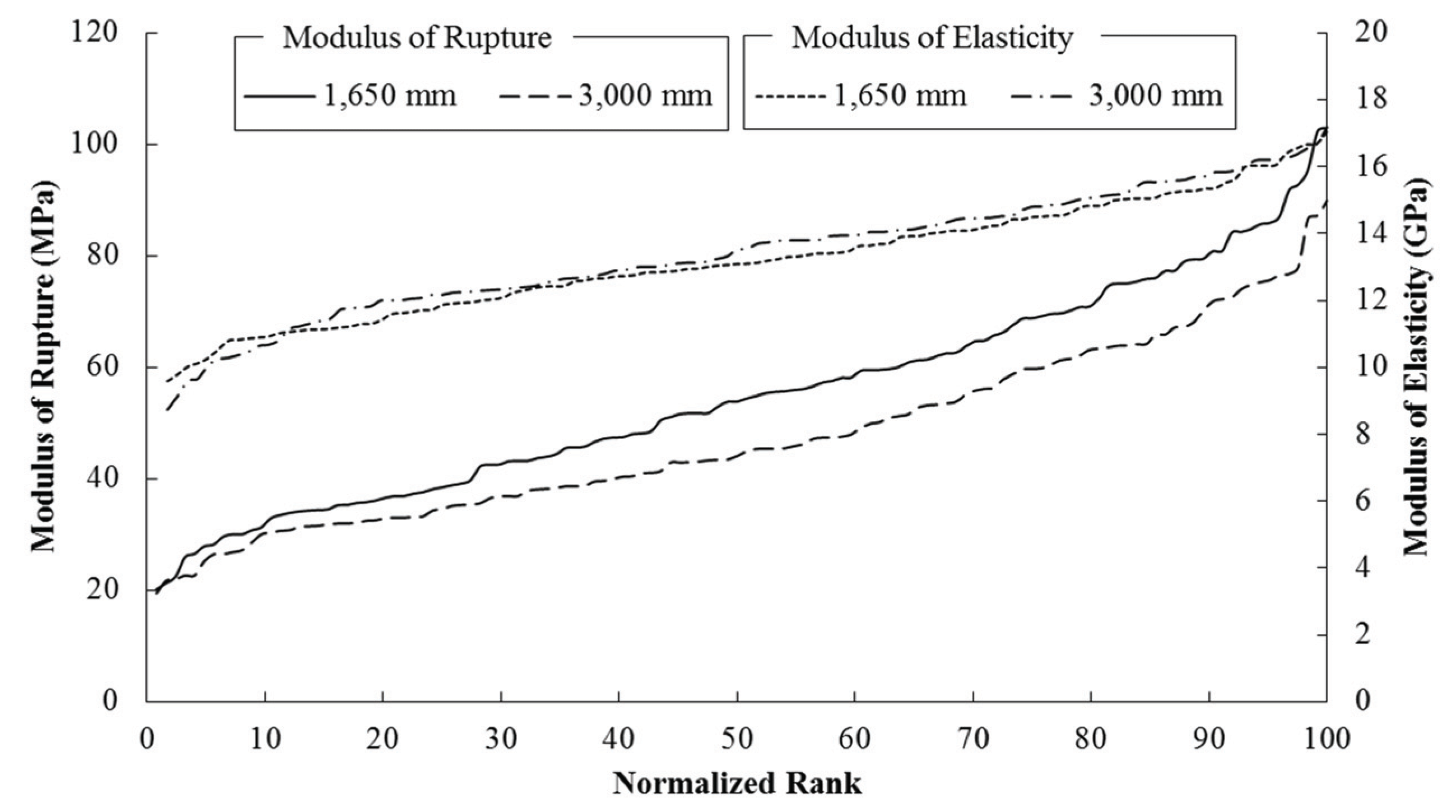
Shown in Table 3 are the fitness distribution test results on the bending strength, which was conducted to determine the standard allowable stress change of visually graded No. 1 lumber by span length. The chi-square test at 5% of significance level showed that at the span length of 1,650 mm, the result followed the normal, lognormal, and Weibull distributions whereas at the span length of 3,000 mm, only the lognormal distribution was fit. Since the 5% lower limit of bending strength can differ by the fitness distribution, it was calculated by using the lognormal distribution determined to be fit commonly in both span lengths. At 1,650 mm, 5% lower limit was 28.65 MPa whereas at 3,000 mm, it was 25.70 MPa so that, like the average bending strength, the longer the span length, the lower the 5% lower limit became. The difference between the average bending strength and the 5% lower limit of bending strength based on span length was 7.44 MPa and 2.95 MPa, respectively, showing that, as in Fig. 2, the increase in the percentage led to the increase in the difference.

Table 3. Results of Chi-Square goodness of fit test according to span length

Span length (mm)	1,650			3,000
Distribution	Normal	Lognormal	Weibull	Normal	Lognormal	Weibull
Test statistic	6.384	5.432	5.128	15.856	7.322	14.092
Significant level		0.05			0.05
Degree of freedom	5	5	5	5	5	5
χ²	11.070	11.070	11.070	11.070	11.070	11.070
P value for χ²test	0.271	0.365	0.400	0.007	0.198	0.015

Download Excel Table

Fig. 2. Normalized rank of modulus of rupture and modulus of elasticity for different span lengths.

Download Original Figure

The study compared the bending standard allowable stress calculated by multiplying 0.475 to the 5% lower limit of the bending strength based on span length and the design allowable stress, which was produced by multiplying the size coefficient 1.5, proposed by KS F 2162, to the standard allowable stress of the grade No. 1 larch, proposed by the dimension and quality standards of lumber by the National Institute of Forest Science. The standard allowable stress at 1,650 mm and 3,000 mm was 13.61 MPa and 12.21 MPa, respectively; conversely, the design allowable stress of No. 1 grade larch was 11.7 MPa, lower than the standard allowable stress by span length (Table 4). It is believed that this is because the standard allowable stress proposed by the lumber dimension and quality standards of the National Institute of Forest Science was derived from clear wood specimens. Kong and Jeong (2015) reported that since the strength reduction ratio by grade applied to the allowable stress calculation for non-defect small specimens was set high, resulting in a value lower than the allowable stress value by lumber grade.

Table 4. Comparison of allowable bending stress of larch between test result and value in standard

Span length (mm)	Test result (MPa)		Allowable stress in standard1)(MPa)
Span length (mm)	5th percentile	Allowable stress	No. 1	Size-adjusted value
1,650	28.65	13.61	7.8	11.7
3,000	25.70	12.21	7.8	11.7

¹⁾ Notification of 2016: Specification and quality standards of lumber

Download Excel Table

On the contrary, as shown in Table 2 and Fig. 2, the average modulus of elasticity of visually graded No. 1 larch lumber, tends to increase as the span length increases, but there was no significant difference by span length. Madsen (1992) studied the change of the modulus of elasticity by four different span lengthto- depth ratios (12, 18.3, 25.7, and 38.6) in the bending test of a 38×89 mm lumber specimen, the result of which verified the result of this study, that is, the increase in the span length increased the modulus of the average bending elasticity. Here, the same tendency was reported despite that the removal of the effect of the shear deformation changed the modulus of elasticity. While no clear reason for the change of the modulus of the elasticity by span length was given, Barrett et al. (1994) reported that when the span length-depth ratio was small and the ratio of the modulus of elasticity to the modulus of stiffness, including shear deformation, was large, the span length-depth ratio made a huge effect on the modulus of elasticity including shear deformation. However, it was also reported that the ratio of the modulus of elasticity and the modulus of stiffness including shear deformation would change, and therefore, it is believed that additional research would be necessary on the change of the modulus of elasticity by span length on the bending lumber.

It was shown that in bending performance, the span length changed bending strength more than the modulus of elasticity. Such a result can be explained by the weakest link failure theory (Weibull, 1993), which was developed under the assumption that the natural change of the strength properties in lumber is arbitrary and is not related to each other. In a zone under high stress, the probability that weaker areas are to be included would increase as the size of materials increases, and therefore, the strength decreases in inversion to the increase in the size of the material. As such, the phenomenon where the properties of a material change by the size of the material is called size effect, which is known to increase in the strength that shows brittle failure mode due to defects or weak parts in the material rather than in the modulus of elasticity, which has the concept of the mean average (Hwang et al., 2003). As such, the span length changed bending strength more drastically in the bending performance.

To consider the size effect in lumber, ASTM D1990 proposes an equation that converts the strength data acquired by the test to a specific size. For the bending strength, the equation in ASTM D1990 uses 0.14 as the modulus of size in length. Barrett et al. (1995) reported that in the visually graded Hem-Fir and S-P-F, the modulus of size in length was 0.18 and 0.16, respectively. Within the 5% lower limit of bending strength, acquired by the test of this study, the modulus of size in length, acquired by the regressive analysis of the log value in strength and the log value in length (Barrett et al., 1995) was 0.18, showing that as in Fig. 3, larch had a large size effect when compared to ASTM D1990.

Fig. 3. Linear regression of logarithm of strength against logarithm of span length. Here, absolute value in slope indicates a length factor.

Download Original Figure

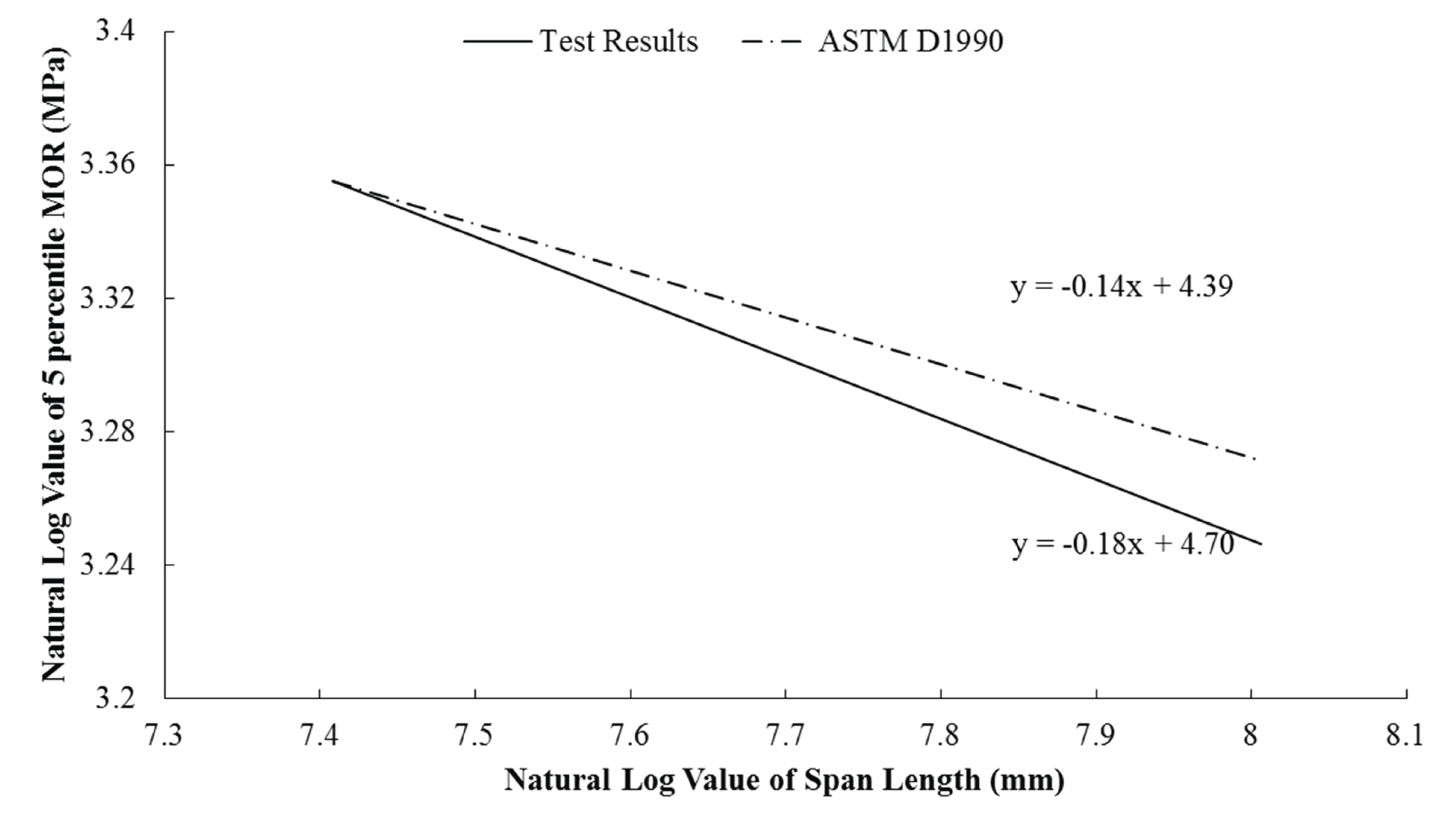
While there has been consistent research on the bending test for lumber in South Korea (Park et al., 2010; Pang et al., 2013), Oh (2014), which compared the value from literature to the modulus of size in length through the regression analysis of the log value in strength and the log value in depth in bending strength, is the only research on size effect. Thus, it is determined that additional research on size effect is necessary. Particularly, it is believed that it is possible to include an equation that can consider size effect as in ASTM D1990 or to make revisions in which to include an equation to consider size effect as well as limiting the span length-to-depth ratio in KS F 2150. Considering that the length of generally used lumber is 3,600 mm, various types of span length can be selected based on the cross-section of the produced lumber, and therefore, it is expected that the problem of different results of bending tests even by following the KS standards could be compensated. Furthermore, the strength values acquired from lumber in various sizes can be reflected to the design values.

4. CONCLUSION

The study conducted a bending test on 38 × 89 mm lumber to determine the effect of span length on the bending performance of structural lumber. The result showed a significant change of bending strength among the bending performance properties by span length within 5% of significance level. The 5% lower limit of the bending strength increased as the span length shortened, as in 28.65 MPa at 1,650 mm, and 25.70 MPa at 3,000 mm. It is believed that this was due to size effect, and it is determined that a corresponding compensation method of strength values by size would need to be included in KS F 2150. It is expected that in this way, various strength values from different sizes of lumber can be reflected to design values.

Appendices

APPENDIX (Korean Version)

4점 휨 시험에서 지간 거리에 따른 2×4 낙엽송 제재목의 휨 성능 변화

요약 : 4점 휨 시험에서 지간 길이에 따른 낙엽송 제재목의 휨 성능 변화를 알아보기 위하여 연구를 진행하였다. 연구에 사용된 시험편의 크기는 38(너비) × 89(깊이) × 3,600(길이) mm³이며, 평균 기건 밀도와 함수율은 각각 543.5 kg/m³, 10.5% 이었다. 낙엽송 육안 등급 1등급 248본을 두 그룹으로 나눠, 지간 거리 1,650 mm와 3,000 mm에서 휨 실험을 진행하여 휨 강도와 휨 탄성계수를 도출하였다. 휨 탄성계수는 유의 수준 5%에서 지간 거리에 따라 차이가 없다고 판단된 반면 휨 강도는 차이가 있었으며, 지간에 반비례하였다. 지간 거리 1,650와 3,000 mm에서 휨 강도의 5% 하한치는 각각 28.65와 25.70 MPa로 확인되었다. 지간 거리에 따른 휨 강도 차이는 백분위 수가 증가함에 따라 커지는 것으로 확인되었으며, 이는 와이블 최약 링크 파손 이론에 의한 치수 효과 때문으로 사료된다. 따라서 지간 대 깊이 비가 15 이상으로만 제한되어 있는 목구조용 실대재 휨 시험법(KS F 2150)에 치수 효과를 고려할 수 있는 방법이 포함되어야 할 것으로 판단된다. 이를 통해 다양한 치수의 제재목에 서 얻어지는 강도를 설계 값에 반영할 수 있을 것으로 기대된다.

1. 서 론

목조 건축 건설 시장은 해마다 증가하고 있으며, 2017년의 목조 건축 허가 수는 약 17,000 동에 이르렀다(Ministry of Land, Infrastructure and Transport, 2017). 이는 조적조 건축 허가 수의 약 2배에 해당하는 것으로, 건축 시장에서 목조 건축이 차지하는 비율이 적지 않다고 할 수 있다. 목조 건축 건설 시장에서 벽이나 바닥덮개 내부에 보, 스터드 또는 장선과 같이 상대적으로 작은 구조 요소가 일정 간격으로 놓여진 구조체를 사용하는 경골 목조 건축물이 큰 비중을 차지하고 있으며, 이에 따라 표준 치수를 가지고 있는 규격 제재목의 성능은 매우 중요하다고 할 수 있다.

목조 건축 건설 시장이 꾸준히 증가함에도 불구하고 우리나라 국내 제재목은 구조용으로 거의 사용되지 않고 있다. 대신 경골 목조 건축물에 사용되는 제재목은 북아메리카, 뉴질랜드, 일본 등에서 주로 수입되어 공급된다. 이는 산림의 활용보다는 산림 녹화 정책이 우선시 되어, 국내 제재목의 활용이 등한시 되었기 때문이라고 생각된다. 그러나 이러한 상황은 산림 녹화 정책으로 형성된 풍부한 자원의 이용 필요성 증가와 유엔기후변화협약(UNFCCC)을 기초로 합의된 파리 협정을 우리나라가 채택함에 따라 달라지고 있다. 따라서 목재의 탄소고정 효과를 지속할 수 있는 고부가가치 재료로서, 국내 제재목 사용 증가가 기대된다. 구조용재로 국내 제재목을 사용하기 위해서는 정확한 설계 값이 필요하다. 정확한 설계 값은 건축물의 구조 안정성을 보장할 뿐만 아니라 공학 목재를 적절히 제조하는데 필수적으로 요구되기 때문이다. 이러한 설계 값은 표준 시험 방법을 통하여 결정된다. 특히 목재는 고유의 결함을 가지고 있어 물성의 변이가 크고, 시험 조건에 영향을 받기 때문에 표준 시험 방법이 중요하다.

시험 방법에 따른 목재의 기계적 물성에 변화에 대한 연구는 꾸준히 진행되고 있다. Gerhards와 Link(1986)은 하중 재하 속도가 제재목의 휨 강도에 미치는 영향에 대하여 조사하였으며, 제재목의 평균 휨 강도는 하중 재하 속도의 로그 값에 거의 선형적으로 증가한다고 보고하였다. Schneeweiß와 Felber(2013)는 4점 하중 시험과 중앙 하중 시험 하에서 참나무와 가문비나 무에 대하여 휨 시험을 진행하였으며, 중앙 하중 시험에서 얻어진 휨 강도 값보다 4점 하중 시험에서 얻어진 휨 강도 값이 낮다는 것을 확인하였다. Bechtel와 Norris(1959)는 10에서 14까지의 지간 대 깊이의 비에서 무결점 소시편 시트카 가문비나무 (Sitka spruce)의 휨 강도는 지간 대 깊이의 비가 증가함에 따라 증가함을 보고하였다. Isaksson(1999) 또한 구조용 제재목으로 만들어진 보의 하중 지지 성능과 지간에 대한 연구를 진행하였으며, 지간의 길이가 증가할수록 보의 하중 지지 성능은 감소한다 고 보고 하였다.

우리나라에서 제재목의 휨 시험 방법은 한국산업규격(KS)의 목구조용 실대재의 휨 시험 방법, KS F 2150를 통하여 규정하고 있다. KS F 2150의 시험 조건은 해외 기준과 대동소이하나, 지간 대 깊이 비에 대한 내용은 차이가 있다. KS F 2150는 지간 대 깊이 비 15 이상에서 자유롭게 지간을 설정할 수 있다고 제시되어 앞선 연구 결과를 미뤄보았을 때 의문점이 있다. 따라서 본 논문에서는 지간 대 깊이의 비가 육안 등급 구분된 낙엽송 제재목의 휨 강도에 미치는 영향에 대한 연구를 진행하였다.

2. 재료 및 방법

2.1. 재료

국내에서 식재량이 풍부하고 구조적 목적으로 선호되는 낙엽송(Lartix kaempferi (Lamb.) Carriere)을 시험 수종으로 선택하였 다. 열기 건조된 2 × 4 낙엽송 제재목(실제 크기 38(너비) × 89(깊이) × 3,600(길이) mm³)은 산림조합중앙회 중부목재유통센터(경기 여주)에서 구매하였다. 구매한 2 × 4 낙엽송 제재목 수는 550개 이었으며, 육안 등급 구분 결과 1등급으로 판정된 248개의 시험편을 시험에 사용하였다. 육안 등급은 국립산림과학원 고시 목재제품의 규격과 품질 기준에 따라 진행하였으며, 그 기준은 표 1에 제시되어 있다. 육안 등급 1등급 낙엽송 제재목은 항온 항습실(20도, 상대 습도 65%)에 보관하여 평형함수율에 도달하도록 하였다. 시험편의 평균 함수율은 10.5 ± 1.5%이었으며, 평균 기건 밀도는 543.5 ± 62.3 kg/m³이었다.

2.2. 휨 시험 방법

만능 재료 시험기(MTS, 미국)를 이용하여 실대재 4점 휨 시험을 진행하였으며, 두 종류의 지간 거리(1,650과 3,000 mm)를 사용하여 4점 휨 시험에서 지간 거리가 휨 성능에 미치는 영향을 알아보고자 하였다. 이 때 지간 대 깊이 비는 지간 거리 1,650과 3,000 mm에서 각각 18.5와 33.7이었다. KS의 목구조용 실대재의 휨 시험 방법(KS F 2150)에 따라, 각 조건의 휨 시험에서 평균 6분 후에 파괴가 발생하도록 시험 속도를 설정하여 시험을 진행하였다. 휨 시험이 진행되는 동안 변위측정기 (Kyowa, 일본)를 이용하여 지간 사이에서 중립축의 변위를 측정하였다. 측정된 하중과 변위 값을 이용하여 좁은 재면의 휨 강도와 전단 변형이 포함된 탄성계수를 구하였다. 등급에 영향을 미치는 결함은 인장면, 압축면에 관계없이 임의로 하중 지간 사이에 배치시켜 실험을 진행하였다. 그림 1에 휨 시험에 대한 도식이 제시되어 있다.

2.3. 통계 분석

지간 거리에 따라 휨 성능이 변화하는지 확인하기 위해 휨 강도와 휨 탄성계수에 대하여 유의 수준 5%에서 t 검정을 실시하였 다. t 검정을 실시하기 전, 각 지간 거리에 따른 휨 성능 사이에 유의차 검증을 위하여 유의 수준 5%에서 F 검정을 실시하였다. 휨 성능에서 휨 탄성계수는 평균 값을 대표값으로 사용하는 반면, 휨 강도는 5% 하한치를 기반으로 한 기준 허용응력을 대표값으 로 사용한다. 따라서 지간 거리에 따른 휨 강도의 변화를 알아보기 위해 조건에 따른 휨 기준 허용응력을 산출하여 비교하였다. 기준 허용응력을 산출하기 위하여 모수적 방법으로 정규, 대수정규 2모수 와이블(Weibull) 분포를 사용하여 5% 하한치를 계산하였다. 각 분포의 확률 밀도 함수는 다음과 같이 정의된다.

여기서, e=오일러 상수, ln=자연로그, μ=평균, σ =표준 편차, m=lnμ2/σ2+μ2,v=lnσ2/μ2+1, a=척도 모수(scale parameter), 그리고 b=형상 모수(shape parameter). 각 분포 확률 밀도 함수의 적합도 검정을 통하여, 지간 거리에 따른 휨 강도 분포 특성을 모두 만족하는 분포에서 휨 강도의 5% 하한치를 산출하였다. 적합도 검정은 유의 수준 5%에서 카이제곱 검정을 이용하여 실시하였다. 정규와 대수정규 분포에서 기준 허용응력을 산출할 때는 95% 신뢰 수준에서 한쪽 오차 한계(0.95)에 대한 k인자로 서 1.645를 사용하여 휨 강도의 5% 하한치를 계산하였다. 그 후 침엽수 구조 용재의 허용 성질 결정 방법(KS F 2152)에 제시된 바와 같이, 산출된 휨 강도의 5% 하한치에 정상 하중 기간과 안전 계수를 고려하여 결정된 감소 인자 0.475를 곱한 기준 허용응력을 산출하였다.

3. 결과 및 고찰

지간 거리에 따른 육안 등급 1등급 제재목의 휨 강도 변화를 알아보기 위하여, 휨 시험을 통해 얻어진 최대 하중을 사용하여 휨 강도를 계산하였다. 표 2에 지간 거리에 따른 휨 강도의 통계적 결과가 제시되어 있다. F 검정에서 p 값이 0.070로 유의 수준 5% 보다 높아 지간 거리에 따른 휨 강도의 분산 간의 차이는 통계적으로 유의하지 않았다. 따라서 등분산으로 가정하여 두 조건에 따른 평균 휨 강도의 결과를 t 검정 하였다. 그 결과, p 값이 0.001로 유의 수준 5% 보다 낮아 귀무 가설을 기각하였다. 다시 말해서, 지간 거리에 따라 평균 휨 강도 간의 차이가 존재한다고 결론 내릴 수 있었다. 지간 거리 1,650 mm 시험 조건에서 얻어진 평균 휨 강도는 55.01 MPa로, 지간 거리 3,000 mm 시험 조건에서 얻어진 평균 휨 강도 47.54 MPa보다 크게 나타났다(표 2).

지간 거리에 따른 육안 등급 1등급 제재목의 기준 허용응력 변화를 살펴보기 위한 휨 강도에 대한 적합분포 검정 결과는 표 3과 같다. 유의 수준 5%에서 카이제곱 검정을 한 결과, 지간 거리 1,650 mm에서는 정규, 대수정규, 와이블 분포를 모두 따른다고 판별된 반면, 지간 거리 3,000 mm에서는 대수정규 분포만 적합하다는 결과를 얻었다. 적합분포에 따라 휨 강도의 5% 하한치가 달라질 수 있기 때문에 각 지간 거리에서 공통으로 적합하다고 판정된 대수정규 분포를 이용하여 휨 강도의 5% 하한치를 산출하였다. 지간 거리 1,650 mm에서는 휨 강도의 5% 하한치가 28.65 MPa인 반면, 지간 거리 3,000 mm에서는 25.70 MPa으로 평균 휨 강도와 같이 지간 거리가 길어질수록 5% 하한치가 낮게 나타났다. 지간 거리에 따른 평균 휨 강도의 차이와 휨 강도의 5% 하한치 차는 각각 7.44와 2.95 MPa로 그림 2에서와 같이 백분위 수가 증가함에 따라 차이가 큰 것으로 확인되었다. 지간 거리에 따른 휨 강도의 5% 하한치에 0.475를 곱하여 산출한 휨 기준 허용응력과 국립산림과학원 고시 목재제 품의 규격과 품질 기준에 제시된 낙엽송 1등급의 기준 허용응력에 KS F 2162에 제시되어 있는 치수계수 1.5를 곱한 설계 허용응력과 비교하였다. 지간 거리 1,650와 3,000 mm에서의 기준 허용응력은 각각 13.61와 12.21 MPa이었다. 이에 반하여 낙엽송 1등급의 설계 허용응력은 11.7 MPa으로 지간 거리에 따른 기준 허용응력보다 낮게 나타났다 (표 4). 이는 국립산림과학원 고시 목재제품의 규격과 품질 기준에 제시된 기준 허용응력이 무결점 소시편을 통해 도출된 값이기 때문이라고 사료된다. Kong와 Jeong(2015)은 무결점 소시편의 허용응력산출에 적용되는 등급별 강도감소비가 높게 설정되어있기 때문에 실대재의 등급별 허용응력 값보다 낮은 결과를 보인다고 보고한 바 있다.

이에 비하여, 육안 등급 1등급 낙엽송 제재목의 평균 휨 탄성계수는 표 2와 그림 2에 나와 있는 바와 같이 지간 거리가 길어질수록 평균 휨 탄성계수가 커지는 경향을 나타내었으나 지간 거리에 따라 유의미한 차이를 보이지 않았다. Madsen(1992) 은 단면의 크기 38×89 mm 제재목의 휨 실험에서 네 가지 지간 대 깊이 비(12, 18.3, 25.7, 38.6)에 대한 휨 탄성계수의 변화에 대한 연구 결과를 발표한 바 있으며, 본 연구 결과와 같이 지간의 길이가 길어질수록 평균 휨 탄성계수가 증가함을 확인하였다. 여기서 전단 변형의 영향을 제거하여 지간 대 깊이 비에 따른 휨 탄성계수 변화를 확인하였음에도 불구하고 같은 경향을 보인다고 보고하였다. 지간 거리에 따른 목재의 휨 탄성계수 변화의 정확한 원인은 밝혀진 바 없으나, Barrett 등(1994)은 지간 대 깊이의 비가 작으면서 전단 변형이 포함된 탄성계수와 강성계수의 비가 클 때, 지간 대 깊이의 비는 전단 변형이 포함된 탄성계수에 크게 영향을 미친다고 보고하였다. 그러나 수종과 등급에 따라 전단 변형이 포함된 탄성계수와 강성계수의 비가 달라진다고 보고하고 있기 때문에 목재의 휨 부재에서 지간에 따른 탄성계수의 변화에 대한 추가적인 연구가 필요할 것으로 판단된다. 휨 성능에서 지간 거리에 따른 휨 탄성계수의 변화보다 휨 강도가 더 크게 변화하는 것으로 나타났다. 이러한 결과는 부재 내 강도 물성의 자연적인 변이가 임의적이고 서로 관련이 없다는 가정 아래에서 발전된 와이블 최약 링크 파손 이론(weakest link failure theory) (Weibull, 1939)으로 설명할 수 있다. 높은 응력을 받는 영역에서 더 약한 부위가 포함될 확률은 재료의 크기가 증가할수록 커지기 때문에 재료의 크기 증가에 반비례하여 강도가 감소하게 된다. 이처럼, 재료의 물성의 크기에 따라 변화되는 현상을 치수 효과(size effect)라 하고, 치수 효과는 평균치 개념을 갖는 탄성 계수보다는 결함 또는 재료 취약부가 원인이 되어 취성 파괴 모드를 보이는 강도에서 크게 나타난다고 알려져 있다(Hwang 등, 2003). 그러한 이유로, 휨 성능에서 지간 거리에 따라 휨 강도가 더 크게 변화하였다.

목재에서 발생하는 치수 효과를 고려하기 위하여 ASTM D1990에서는 실험을 통해 얻어진 강도 데이터를 특정 치수로 변환하는 식을 제안하고 있다. 휨 강도에 대하여 ASTM D1990의 식에서는 길이의 치수 계수로 0.14를 사용하고 있다. Barrett 등(1995)은 육안 등급 구분된 Hem-Fir와 S-P-F에서 길이의 치수 계수는 각각 0.18과 0.16이라 보고한 바 있다. 본 실험을 통해 얻어진 휨 강도의 5% 하한치에서, 강도의 로그 값과 길이의 로그 값의 회귀 분석을 통하여 얻어진 길이의 치수 계수(Barrett 등, 1995)는 0.18로, 그림 3과 같이 ASTM D1990과 비교하였을 때 낙엽송이 치수 효과가 큰 것으로 나타났다.

국내 제재목에 대한 실대재 휨 시험은 꾸준히 진행된 바 있으나(Park 등, 2010; Pang 등, 2013), 치수 효과에 대한 연구는 Oh(2014)가 휨 강도에서 강도의 로그 값과 깊이의 로그 값의 회귀 분석을 통해 깊이의 치수 계수를 산출하여 문헌 값과 비교한 연구를 진행한 사례가 유일하다. 이에 대한 추가적인 연구가 필요하다고 판단된다. 추가적인 연구를 통하여 ASTM D1990과 같이 치수 효과를 고려할 수 있는 식을 포함하거나, KS F 2150에서 지간 대 깊이 비를 제한하는 동시에 치수 효과를 고려할 수 있는 식 포함하는 등의 개정이 가능할 것으로 사료된다. 일반적으로 유통되는 제재목의 길이가 3,600 mm인 것을 감안하면, 생산하는 제재목의 단면에 따라 다양한 지간 거리를 선택할 수 있기 때문에 KS에 따라 휨 실험을 진행했음에도 불구하고 결과가 달라질 수 있는 점을 보완할 수 있을 것으로 기대된다. 이를 통하여 다양한 치수의 제재목에서 얻어지는 강도를 설계 값에 반영할 수 있을 것이다.

4. 결 론

지간 거리가 구조용 제재목의 휨 성능에 영향을 미치는지 알아보고자 단면적 38×89 mm 제재목에 대하여 휨 실험을 진행하였 으며, 그 결과 휨 성능 중 휨 강도가 유의 수준 5%에서 유의미하게 지간 거리에 따라 변하는 것을 확인하였다. 휨 강도의 5% 하한치는 지간 거리 1,650 mm에서 28.65 MPa, 3,000 mm에서 25.70 MPa로 지간 거리가 짧아질수록 강도가 증가하였다. 이는 치수 효과에 의한 것으로 사료되며, 이를 고려하여 치수에 따른 강도 값을 보정할 수 있는 방법을 목구조용 실대재 휨 실험 방법, KS F 2150에 포함하여야 할 것으로 판단된다. 이를 동해 다양한 치수의 제재목에서 얻어지는 강도를 설계 값에 반영할 수 있을 것으로 기대된다.

References

American Society for Testing and Materials Standard Practice for Establishing Allowable Properties for Visually-Graded Dimension Lumber from In-Grade Tests of Full-Size Specimens: ASTM D1990. 2016 West Conshohocken, PA: ASTM International. .

Barrett J., Lam F., Lau W. Size effects in visually graded softwood structural lumber. Journal of Materials in Civil Engineering. 1995; 7(1):19-30.

Barrett J.D., Jones E., Lau W. Canadian lumber properties. 1994Canadian Wood Council. .

Bechtel S., Norris C. Strength of wood beams of rectangular cross section as affected by span-depth ratio. 1959 Madison, Wis. .

Gerhards C., Link C.L. Effect of loading rate on bending strength of Douglas-fir 2 by 4's. Forest Products Journal. 1986; 36:63-66.

Hwang T.K., Hong C.S., Kim C.G. Probabilistic fiber stregnth of composite pressure vessel. Composites Research. 2003; 16(6):1-9.

Isaksson T. Modelling the variability of bending strength in structural timber-length and load configuration effects. Doctoral thesis. 1999 Lund, Sweden: Division of structual engineering, Lund University. .

Kong J.H., Jeong G.Y. Review of visual grading and allowable stress determination methodologies for domestic softwood. Journal of the Korean Wood Science and Technology. 2015; 43(1):25-35.

Korean Standard Adjustment factors applied to allowable stresses of structural timber and glued laminated timber: KS F 2162. 2004 Seoul, Korea: Korean Standards Association. .

10.

Korean Standard Method of static bending test for full sized structual lumber: KS F 2150. 2004 Seoul, Korea: Korean Standards Association. .

11.

Madsen B. Structural behavior of timber. 1992Timber Engineering Ltd. .

12.

Ministry of Land，Infrastructure and Transport Statistics on building permisstion and commencement works. 2017.

13.

Notification. Specifications and quality standards of lumber: 2016-8. 2016 Seoul, Korea: National Forest Research Institute. .

14.

Oh S.C. Estimation of Depth Effect on the Bending Strength of Domestic Japanese Larch Structural Lumber using Weibull Weakest Link Theory. Journal of the Korean Wood Science and Technology. 2014; 42(2):112-118.

15.

Pang S-J., Lee J-J., Oh J-K. Evaluation of Allowable Bending Stress of Dimension Lumber; Confidence Levels and Size-adjustment. Journal of the Korean Wood Science and Technology. 2013; 41(5):432-439.

16.

Park C-Y., Pang S-J., Park J-S., Kim K-M., Park M-J., Lee J-J. Study of the distribution properties and LRFD code conversion in Japanese larch. Journal of the Korean Wood Science and Technology. 2010; 38(2):94-100.

17.

Schneeweiß G., Felber S. Review on the bending strength of wood and influencing factors. American Journal of Materials Science. 2013; 3(3):41-54.

18.

Weibull W. A statistical theory of the strength of materials. 1939Ing. Vet. Ak. Handl. .