Dynamic Property of Cross-Laminated Woods Made with Temperate Seven Species

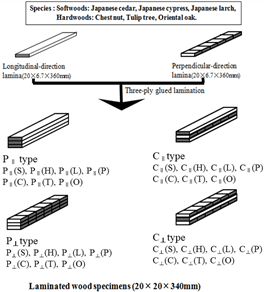
Seven species of temperate softwoods and hardwoods were selected for this study. They included four softwoods: Japanese cedar (density: 400 kg/m³), Japanese cypress (density: 452 kg/m³), Japanese red pine (density: 601 kg/m³) and Japanese larch (density: 604 kg/m³); three hardwoods: chestnut (density: 582 kg/m³), tulip tree (density: 595 kg/m³) and oriental oak (density: 901 kg/m³). Longitudinal-direction laminae of 6.7 (T) × 20 (R) × 360 (L) mm whose long axes were parallel to the grain were made with seven species. Elements of 7.5 (T) × 20 (R) × 180 (L) mm were cut from each seven species, 18 elements from each species were edge-jointed and then cut to 20 mm size in width direction and perpendicular-direction laminae of 6.7 (T) × 360 (R) × 20 (L) mm were made with long axes perpendicular to the grain. The annual ring angles of both laminae were 90^◦. An isocyanate type adhesive (MPU-500) formulated for a room temperature cure was used, and the amount of spread was 300 g/m². The three-ply laminae were pressed under pressure of 0.34 MPa for 24 hours in a room maintained at 20℃ and 65%RH. Fig. 1 shows three-ply parallel- and cross-laminated wood panel specimens tested. P_∥type (P_∥(S), P_∥(H), P_∥(P), P_∥(L), P_∥(C), P_∥(T) and P_∥(O), where S: Japanese cedar, H: Japanese cypress, P: Japanese red pine, L: Japanese larch, C: Chestnut, T: Tulip tree, O: Oriental oak) and P_{⊥type (P⊥(S), P⊥(H), P⊥(P), P⊥(L), P⊥(C), P⊥(T) and P⊥(O)) were the specimens used to measure the bending strength performances parallel and perpendicular to the grain of parallel-laminated wood panels, respectively. C∥ type (C∥(S), C∥(H), C∥(L), C∥(P), C∥(C), C∥(T) and C∥(O)) and C⊥ type (C⊥(S), C⊥(H), C⊥(P), C⊥(L), C⊥(C), C⊥(T) and C⊥(O)) were the specimens used to measure the bending strength performances parallel and perpendicular to the grain of the face laminae of cross-laminated wood panels, respectively. Using a total of seven species of four softwood and three hardwoods, 28 types of parallel- and cross-laminated wood panels were manufactured. A total of 280 laminated specimens, 10 for each type, were prepared to investigate the dynamic behavior.}

Fig. 1. Parallel- and cross-laminated woods specimens made with seven species. S, H, L, P, C, T and O are Japanese cedar, Japanese cypress, Japanese larch, Japanese red pine, chestnut, tulip tree and oriental oak, respectively.

Download Original Figure

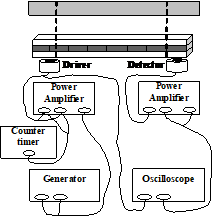
Vibration was induced via a small steel plate attached to the bottom end of 3-ply laminated wood specimens and suspended by two threads at the magnetic driver as shown in Fig. 2. The vibration was received at a small steel plate attached to the other end. The test was made with both ends free. The test apparatus consisted of a sine wave generator (Type 1023, B&K), a universal counter timer (Type 5001, GSP) and an oscilloscope (Type 1740A, HP). The value of the frequency counter timer was recorded when the relative amplitude indicated the highest value on the oscilloscope. Resonance frequency ( f ) and dynamic MOE (MOE_d) were calculated by the following equations (Kataoka and Ono, 1975):

Fig. 2. Schematic diagram of flexural vibration of laminated wood specimens.

Download Original Figure

where f₀ is the value obtained from frequency counter timer, α= 8.2 is_{the value according to chosen vibration type, h isthe thickness of specimen (mm), l is the length of specimen (mm).}

where ρ is density (kg/m³), m = 4.73 is_{the value according to the chosen basic vibration, h isthe thickness of specimen (mm), l is the length of specimen (mm).}

Results of the flexural vibration test under free-free beam condition of parallel- and cross-laminated wood panels made with four softwoods and three hardwoods are shown in Table 1. And Fig. 3. shows the effect of the density on the dynamic MOE of the laminated wood panels.

Fig. 3. Effects of wood species on dynamic MOE (MOE_d) for P_∥, P_⊥, C_∥ and C_⊥ type laminated wood　specimens. S: Japanese cedar, H: Japanese cypress, L: Larch, P: Red pine, C: Chestnut, T: Tulip tree, O: Oriental oak. ▲: Average MOE_d.

Download Original Figure

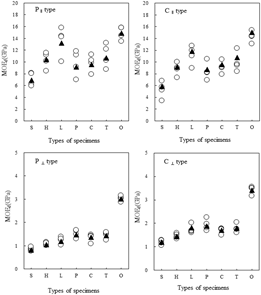
As shown in Fig. 3, in the case of the parallel-laminated wood panel of P_∥ type, the P_∥(O) type which all three layers were composed with oriental oak showed the highest value at 14.9 GPa. P_∥(S) type which all three layers were composed with Japanese cedar showed the lowest value at 6.96 GPa. These values generally showed an increase in the dynamic MOE with an increase in the density of the species, indicating the same density dependence as the static bending MOE (Park et al., 2016). However, the P_∥(P) type which composed of red pine showed relatively low dynamic MOE compared to the density due to much resin and not straight grain. The value was in order of P_∥(O)＞P_∥(L)＞P_∥(T)＞P_∥(H)＞P_∥(C)＞P_∥(P)＞P_∥(S), and it was similar to that of static bending MOE. This value was almost equal to or slightly higher by 0.96 to 1.12 times than the static MOE.

As shown in the lower left of Fig. 3, in the case of P_⊥ type parallel laminated wood panels, P_⊥(O) type composed of all three layers of oriental oak showed a value of 3.01 GPa, showing the highest value. The P_⊥(S) type, where all layers were composed of Japanese cedar, showed the lowest value of 0.829 GPa. These values showed an increase in the dynamic MOE with an increase in the density of the species. This value was significantly lower by 0.09 to 0.20 times than that of the P_∥ type parallel laminated wood panels. The value is in order of P_⊥(O)＞P_⊥(P)＞P_{⊥(T)＞P⊥(C)＞P⊥(L)＞P⊥(H)＞P⊥(S). It was confirmed that the density dependence was higher than that of the P∥ type composed of longitudinal-direction laminae in all three layers. This value was 1.04 - 1.14 times that of the static MOE, which was slightly higher than that of the static MOE. This was consistent with Norimoto's research that dynamic MOE of wood had a higher value of 1.1-1.2 times that of static MOE (Norimoto, 1982).}

As shown in the upper right of Fig. 3, in the case of C_{∥type which was composed of perpendicular-direction laminae in the core and longitudinal-direction laminae in the faces, C∥(O) type with oriental oak longitudinal- and perpendicular-direction laminae in the faces and the core showed the highest value of 14.4 GPa. The C∥(S) type with Japanese cedar longitudinal- and perpendicular-direction laminae in the face and the core showed the lowest value of 5.21 GPa. This value showed a low value of 0.75-0.97 times of P∥type. The values were in the order of C∥(O)＞C∥(L)＞C∥(T)＞C∥(C)＞C∥(H)＞C∥(P)＞C∥(S), and overall, it was confirmed that the dynamic MOE increased with increasing density of the species. However, It was confirmed that in the case of the C∥(P) type composed of the face and the core of red pine longitudinal- and perpendicular-direction laminae, the value showed a lower value compared to the density of the species like the P∥type. It was confirmed that this value was 0.93-1.04 times the value of the static MOE, which was almost the same as or slightly higher than that of the static MOE. And it was also slightly lower than the P∥type.}

As shown in the lower right of Fig. 3, in the C_⊥ type cross-laminated wood panel which was composed of longitudinal-direction laminae in the faces and perpendicular-direction lamina in the core, the C_⊥(O) type with oriental oak in the faces and the core has the highest value of 3.42 GPa. The C_⊥(S) type with Japanese cedar in the faces and the core showed the lowest value of 1.20 GPa. Like the P_⊥ type parallel laminated wood panels, this value increased in proportion to the density of the species, and the density dependence showed a clearer tendency than that of the P_∥ type. The dynamic MOE was 1.3 to 1.5 times higher than that of the P_⊥ type by arranging longitudinal- direction lamina in the core of the P_⊥ type with perpendicular-direction laminae in all three layers. The value was in order of C_⊥(O)＞C_⊥(P)＞C_⊥(L)＞C_⊥(T)＞C_⊥(C)＞C_⊥(H)＞C_⊥(S), and according to density increase, the change of the dynamic MOE showed a similar tendency to that of the P_⊥ type, but the extent of the increase was slightly lower than that of the P_⊥ type. It was confirmed that this value represents a high value of 2-11% of the static MOE, which was almost consistent with the study of Norimoto (1982).

The degree of anisotropy for the laminated wood panels expressed as the ratio of the dynamic MOE perpendicular to the grain of face laminae versus that parallel to the grain of the face laminae was Japanese cedar 1: 0.119 to 0.230, Japanese cypress 1: 0.101 to 0.165, Japanese larch 1: 0.090 to 0.164, Japanese red pine 1: 0.162~0.228, chestnut 1: 0.143~0.189, tulip tree 1: 0.136~0.191, oriental oak 1: 0.202~0.238. It was found that the anisotropy significantly decreased by cross-laminating.

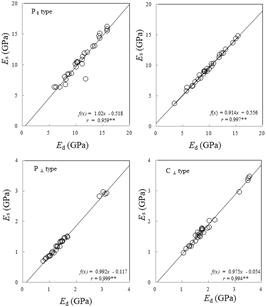
Least squares regression analyses were conducted to examine the relation dynamic MOE by flexural vibration and static bending strength performances, and the derived regression parameters are summarized in Table 2. The relation between the dynamic MOE and static bending MOE of parallel- and cross-laminated wood panels is shown in Fig. 4. In both parallel-laminated wood panels of P_{∥and P⊥ types and cross-laminated wood panels of C⊥and C∥types, a very strong correlation with a significance level of 1% was found between the dynamic MOE and the static bending MOE. The correlation coefficient showed very high values of 𝑟 = 0.959 in P∥ type, 𝑟 = 0.999 in P⊥ type, 𝑟 = 0.997 in C∥ type, and 𝑟 = 0.994 in C⊥ type. This results agreed with various previous researches for solid wood and wood-based materials which there was a high correlation between dynamic MOE and static MOE (Mastumoto and Tsutsumi, 1968; Norimoto, 1982; Bender et al., 1990; Lee et al., 1997; Ayarkwa et al., 2001; Park et al., 2004; Park and Byeon, 2006; Byeon et al., 2005a). This result indicated that the static bending modulus could be predicted nondestructively through the dynamic MOE.}

Fig. 4. Relation between dynamic MOE and static bending MOE of parallel- and cross-laminated wood panels made with seven species. **: Significant at 1% level.

Download Original Figure

The relationship between dynamic MOE and bending proportional limit stress of parallel- and cross- laminated wood panels is shown in Fig. 5. In both parallel-laminated wood panels and cross-laminated wood panels, a very strong correlation with a significance level of 1% was found between the dynamic MOE and the static bending proportional limit stress like the relation between dynamic MOE and static bending MOE. The correlation coefficient showed very high values of 𝑟 = 0.912 in P _|| type, 𝑟 = 0.899 in P_⊥ type, 𝑟 = 0.964 in C_∥ type, and 𝑟 = 0.865 in C_⊥ type. From this result, it was confirmed that the static bending proportional limit stress could be predicted non-destructively through the dynamic MOE.

Fig. 5. Relation between dynamic MOE and bending proportional limit stress of parallel- and cross-laminated wood panels made with seven species. **: Significant at 1% level.

Download Original Figure

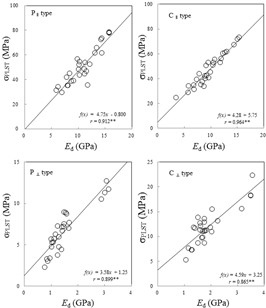
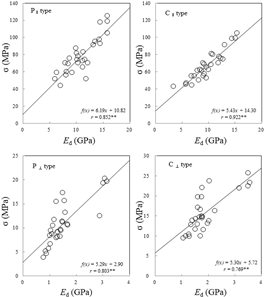
Fig. 6 shows relationship between dynamic MOE and static bending strength of parallel- and cross-laminated wood panels. There was a strong correlation between dynamic MOE and static bending strength like the relations between dynamic MOE and static bending MOE. The correlation coefficient showed very high values of 𝑟 = 0.852 in P_∥ type, 𝑟 = 0.803 in P_⊥ type, 𝑟 = 0.923 in C_∥ type, and 𝑟 = 0.769 in C_⊥ type. It was found that the extent of the relation was stronger in the laminated wood panels with longitudinal- direction laminae in the faces than in that with perpendicular-direction laminae in the faces. This value was higher than the result of a previous study (Park et al., 2011) on the prediction of the bending strength performance of hybrid board composed of green tea and wood fiber by flexural vibration, and was similar to previous study for the laminated wood panels composed of Japanese cedar and beech longitudinal-direction laminae and five species perpendicular-direction laminae (Park and Byeon, 2006). Also, this result agreed with various previous reports which there was a high correlation both dynamic MOE and static bending strength for the wood and wood-based materials (Nakayama, 1975; Bender et al., 1990; Ayarkwa, 2001; Park et al., 2004; 2006; Byeon et al., 2005a). Although the correlation coefficient between the dynamic MOE and the static bending strength was lower than those between dynamic MOE and the static bending MOE or the static bending proportional limit stress, high significance was recognized at the reliability level of 1%. From this result, it was found that static bending strength could be predicted non-destructively through the dynamic MOE like static bending MOE.

Fig. 6. Relation between dynamic MOE and static bending MOR of parallel- and laminated wood panels made with seven species. ** : Significant at 1% level.

Download Original Figure