1. INTRODUCTION
The methods for evaluating the structure and the size of pore in porous materials can be classified into the intrusion method and the extrusion method. Intrusion method is to measure the accumulated volume of a non-wetting liquid to penetrate into pores as pressure increases when pressure is applied to specimens immersed in non-wetting liquid in a chamber. Mercury was used as a non-wetting liquid for the most porous materials. This method is usually called mercury intrusion porosimetry (MIP). The radius of pore is calculated by the Washburn equation (Washburn 1921) based on the surface tension, contact angle and pressure of mercury.
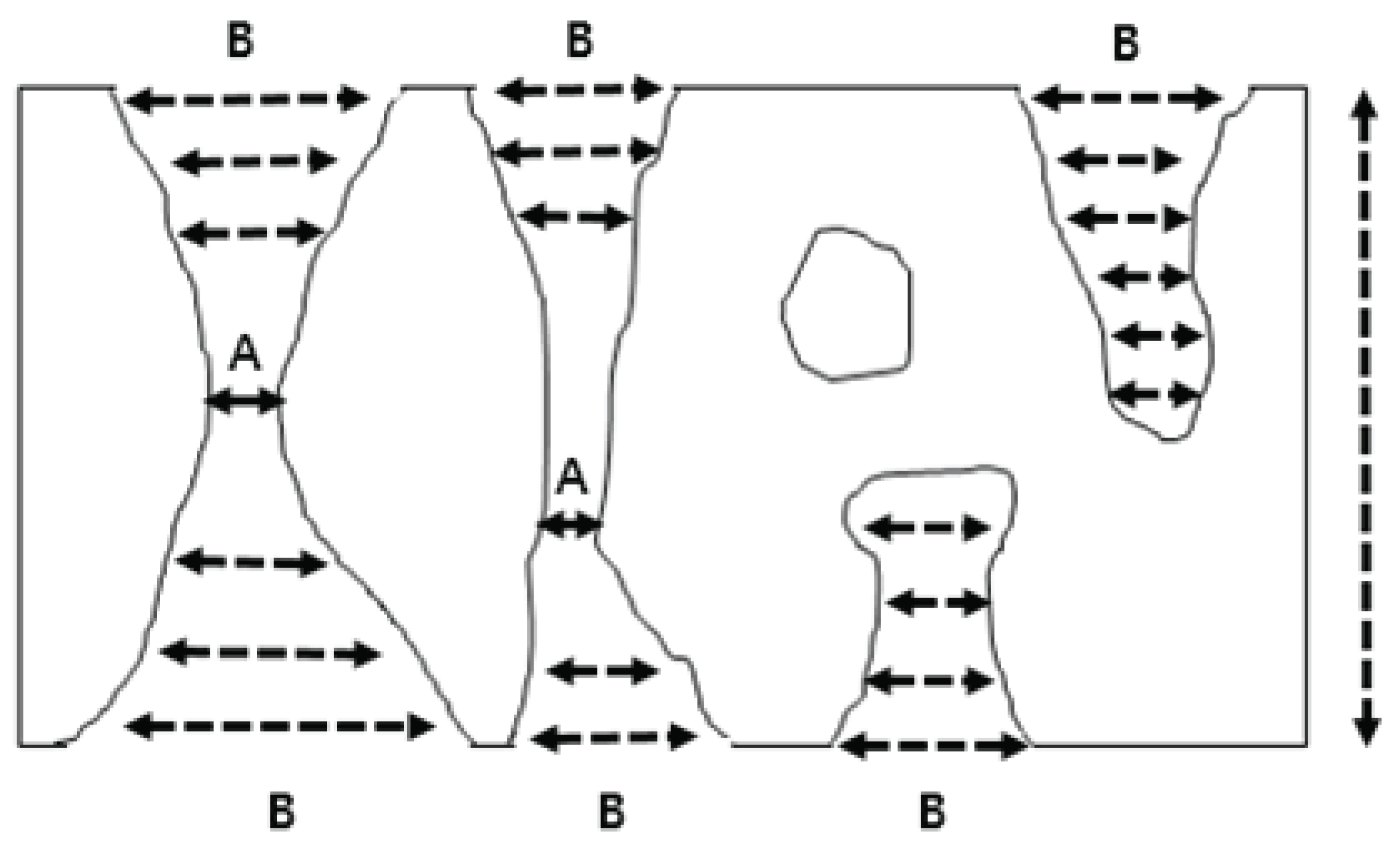
Extrusion method is to measure the pore size through the measurement of pressure when the wetting liquid is extruded by the pressure of air, which is applied after the inside pore is wetted by the wetting liquid that easily penetrates inside pores due to the low surface tension. The pressure at which the wetting liquid was extruded was calculated by Washburn equation. This method is usually called capillary flow porometry (CFP). As shown in Fig. 1, according to IUPAC (International Union of Pure and Applied Chemistry) the measurement area of pores are divided into through pore, blind pore and closed pore.
Jena et al. (2001) analyzed that the pore size of three kinds of battery separator materials measured by MIP and CFP, and reported pore sizes measured by different instruments are different. The diameter of median pore measured by MIP was larger than mean pore diameter measured by CFP.
Jena and Gupta (2005) analyzed the pore structure of nanofiber mats with MIP, Liquid extrusion porosimetry (LEP), and CFP, and reported that the MIP uses high surface tension mercury to impregnate mercury into the pores, which requires high pressure, that causes distortion of the pore structure, but LEP shows good reproducibility without distortion of pore structure due to using low pressures. The CFP is also confirmed that the pore throat diameter can be measured by minimizing the change of the pore structure by using the liquid with low surface tension.
Gribble et al. (2011) present fundamentals and quantitative comparisons between the techniques of CFP, MIP and image analysis for void network modelling for seven types of filter, chosen to encompass the range of simple to complex void structure.
Gigac et al. (2017) compared the pore structure and the size of five kinds of papers using MIP, CFP and reported that the pore size measured by MIP was larger than that measured by CFP because the pore size was presented through calculating the pore volume of through pore and the blind pore in MIP while only constricted part of through pore was measured in CFP.
In the wood industry, the MIP was mainly used to measure the pore volume and pore size (Stayton and Hart, 1965; Lnui and Nakato, 1973; Schneider and Wagner, 1974; Schneider, 1979, 1983; Hösli and Orfila, 1985; Junghans et al., 2005; Pfriem et al., 2009; Plötze and Niemz, 2011).
The primary study was Stayton and Hart (1965) which reported the size, volume, and porosity of pores in wood by pressurizing mercury at 3000 psi in softwood using MIP.
Schneider (1979) reported that the pore size of 30 kinds of European wood specimens could be classified margo capillaries (0.1-0.7 um), lumen radii (0.1-5 um) and 5 um or more using MIP. Michael Plötze and Peter Niemz (2011) reported that the pore size distribution of 24 species of wood which was measured by MIP, and their pore size was classified as macropore (radius 58-2 um and 2-0.5 um), mesopore (500-80 nm) and micropore (80-18 nm).
Stamm (1931) reported that the pore size result measured on the cross-section of the heartwood and sapwood of Slash pine (Pinus caribaea) using the bubble point method, which is the method of measuring the maximum pore size of CFP, the pore size of heartwood is smaller than sapwood.
Kang et al. (2010) reported the relationship between pore size of yellow poplar wood estimated by CFP and the sound absorption rate of wood estimated by transfer function method. Also, Kang et al. (2011) reported the gas permeability of control and steam explosion treated yellow poplar wood specimens by CFP method.
Kang et al. (2018) reported that the pore size of Malas (Homalium foetidum) measured using CFP for heat treated specimens treated for 3 hours at 190 °C and non-heat treated specimens. The maximum pore size diameter after the heat treatment was 13.3 um to 71.8 um, the mean flow pore size was 13.3 to 27.4 um.
In previous studies, MIP and CFP have been widely used for measuring pore size of wood, however, report on comparing MIP and CFP for the estimating of pore size on the same wood materials were rarely found. On the other hand, in case of domestic wood, there are many studies on the anatomical features of wood using microscope. (Lee et al., 2008; Lee et al., 2009, Lee et al., 2011; Qi et al., 2016; Jeon et al., 2018) However, there are few cases of studies on the pore characteristics of domestic wood using CFP or MIP.
The pore characteristics measured by different methods influenced by different measurement principles. The pore size of wood was evaluated using the MIP and CFP after the pore morphology of wood surface was observed by SEM. The purpose of this study is to analyze the pore structure of wood in detail by MIP and CFP, also to investigate the correlation between pore size and gas permeability in MIP and CFP.
These results could be used as meaningful data for understanding pore structures of wood as a porous material. Also, it will be helpful for understanding wood property improvement through chemical impregnation, and for estimating sound absorption properties of wood.
2. MATERIALS and METHODS
Eleven species of domestic log cross sections with the thickness of 10mm were cut from logs (Table 1) and dried at room temperature for over a year, then the cylindrical specimens with the diameter of 15 mm were prepared by rotary lathing. The specimens were sealed by epoxy resin applied hollow acrylic cylinder to permit fluid flow to only longitudinal direction of specimen (Fig. 2).
In order to observe the pore morphology of the cross-section of wood, specimens were cut about 5 x 5 mm, and the surface was smoothed out using a microtome (Model: HM400S, Microm GmbH, Germany). They were coated with gold ion using ion sputter at 12 mV (Fig. 3) and observed at an acceleration voltage of 10 KV and 400 magnification using scanning electron microscope (Model: Genesis-1000, Emcrafts, Korea).
Mercury intrusion porosimeter (Model: AutoPore V 9600, Micrometrics, USA) was used to measure the pores of specimens according to ASTM D4284-12. ASTM D4404-10, ASTM UOP578-11 etc. The relationship between the pressure inside pores and the pore size was determined by Washburn equation;
where,
The pore size of specimens was measured using a capillary flow porometer (Model: CFP-1200AEL, Porous Material Inc, USA) according to the method of ASTM F-316-11. Galwick (surface tension: 15.9 dyne/cm), which is easily wetted, was used as a wetting liquid in this measurement. The pressure at that wetting liquid was extruded was determined by Washburn equation(Washburn, 1921).
where,
D : Diameter of pore for assuming the pore to be cylindrical (mm)
p : Differential pressure (N/m2)
γ : Surface tension for Galwick (mN/m)
θ : Contact angle of Galwick (°)
These measurement method for pore size use the same equation. But the sign of the equation is different. Since MIP is liquid intrusion, so it has a (-) sign, in case of CFP is liquid extrusion, the equation has a (+) sign. (Jena et al., 2001)
Darcy permeability was measured using a capillary flow porometer (Model: CFP-1200AEL, Porous Material Inc, USA). The change in flow rate due to change in pressure was measured while the pressure was perpendicularly increased to the O-ring sealed on the side face of specimen in chamber and converted as a Darcy permeability constant.
where,
3. RESULTS and DISCUSSION
The pore morphology on the cross section of the specimens are displayed in Fig. 4.

Japanese larch (a) and Korean red pine (e) are softwoods and cross-sectional pore structures are classified as tracheid of early wood and tracheid of latewood. The tracheid of early wood has larger pore sizes and are more porous than tracheid of latewood.
Retail ash (b), Paulownia (c), Japanese elm (i) and Amur maackia (k) are ring-porous hardwoods. The early wood vessels are much larger than Latewood.
Manchurian walnut (d) and Lime tree (j) are semi-ring porous hardwood. They are similar to diffuse porous hardwood, it has some features of ring porous hardwood.
Birch (f), Painted maple (g) and Three-flowered maple (h) are diffuse porous hardwood.
Generally, the size and distribution of vessels of the growth rings are constant.
The results of measurement by MIP are shown in Fig. 5. The median pore diameter measured by volume analysis was applied in this measurement because the specific surface area in MIP was thought to be less accurate according to previous research. (Jena et al., 2001). The porosity measured by MIP did not include the closed pore because mercury could not penetrate the closed pore.

If the pore size distribution is very uniform, the larger the pore size, the greater the porosity. However wood is a natural porous material and non-uniform material, which does not show this feature. There was no correlation between pore size and porosity in the wood samples used in this study. The median pore diameter measured by volume analysis of the Lime tree was 9.45494 um, showing the largest pore size among the 11 samples, but the porosity was the second largest at 53.51 %. On the other hand, the median pore diameter by volume of Manchurian walnut was 0.18449 um, which was relatively small pore size among 11 samples, but the porosity (%) was 60.92 %, which was the largest among 11 samples.
The results of measurement of specimens by CFP are shown in Fig. 6. The pore size was mean flow pore size calculated at mean flow pore pressure which was at the intersection point between the maximum pore size obtained from bubble point pressure and the wet curve and the half dry curve.
The Amur maackia had the largest pore size among the 11 samples with maximum pore size and mean flow pore diameter of 36 um and 12.5 um. The maximum pore sizes of the Japanese larch and Korean red pine were 0.504 um and 2.565 um, respectively. The mean flow pore diameters were 0.189 um and 0.2254 um, respectively.
The pore size of softwood was smaller than that of hardwood, which is consistent with the anatomical characteristics of wood. In CFP, however, the constricted part of the pores is measured, which is much smaller than the pore size seen by the SEM.
The permeability on cross section of specimens is shown in Fig. 7.
The Darcy permeability in the wood cross section was the largest at 3.9363 Darcy as Amur maakia, as well as the pore size measured by CFP. Japanese larch, softwood, was the smallest at 0.02181 Darcy.
According to other researches Jena et al. (2001), Jena and Gupta (2005), Gribble et al. (2011), and Gigac et al. (2017), it was generally thought that the pore size measured by MIP was larger than that measured by the methods of CFP, because pore size was calculated based on the pore volume in MIP while the constricted part of through pore was measured in CFP. However, in this study, the tendency was reversed as shown in Fig. 8, the pore size measured by the method of CFP was larger than that the pore size measured by the methods of MIP except for Lime tree, Korean red pine and Paulownia.
It can be considered that the pore structure of wood is different from the porous materials (battery separator, filter, paper) of the previous studies.
During analysis, mercury permeated from tracheid in the longitudinal direction of coniferous wood and could permeate ray tracheid as the pressure is increased while mercury permeated from the vessel element in the longitudinal direction of deciduous wood and could permeate inside pit in horizontal direction of vessel element as pressure is increased.
Moreover, the minute pores on wood surface could also be measured because mercury could permeate between cell lumen. The parts of wood with tyloses that blocked the pit canal and resulted in the pit being closed, which closed the vessel and prevented fluid to flow, and could not be measured.
On the other hand, the bordered pit pair in the longitudinal direction of tracheid cylindrical cell of coniferous wood was estimated as the narrowest pore in case of CFP method because the CFP measured constricted part (throat pore) of through pore. The pores in perforation plate of deciduous wood were possibly measured by CFP. This method could not measure the aspirated pit, ray tracheid cell in horizontal direction, the cell lumen with tylosis, therefore, the pore size in wood measured by CFP was larger than that measured by MIP unlike other porous materials.
From the results of the comparing gas permeability with CFP and MIP, we could not find out any correlation between gas permeability from CFP and the porosity, the pore size measured by MIP.
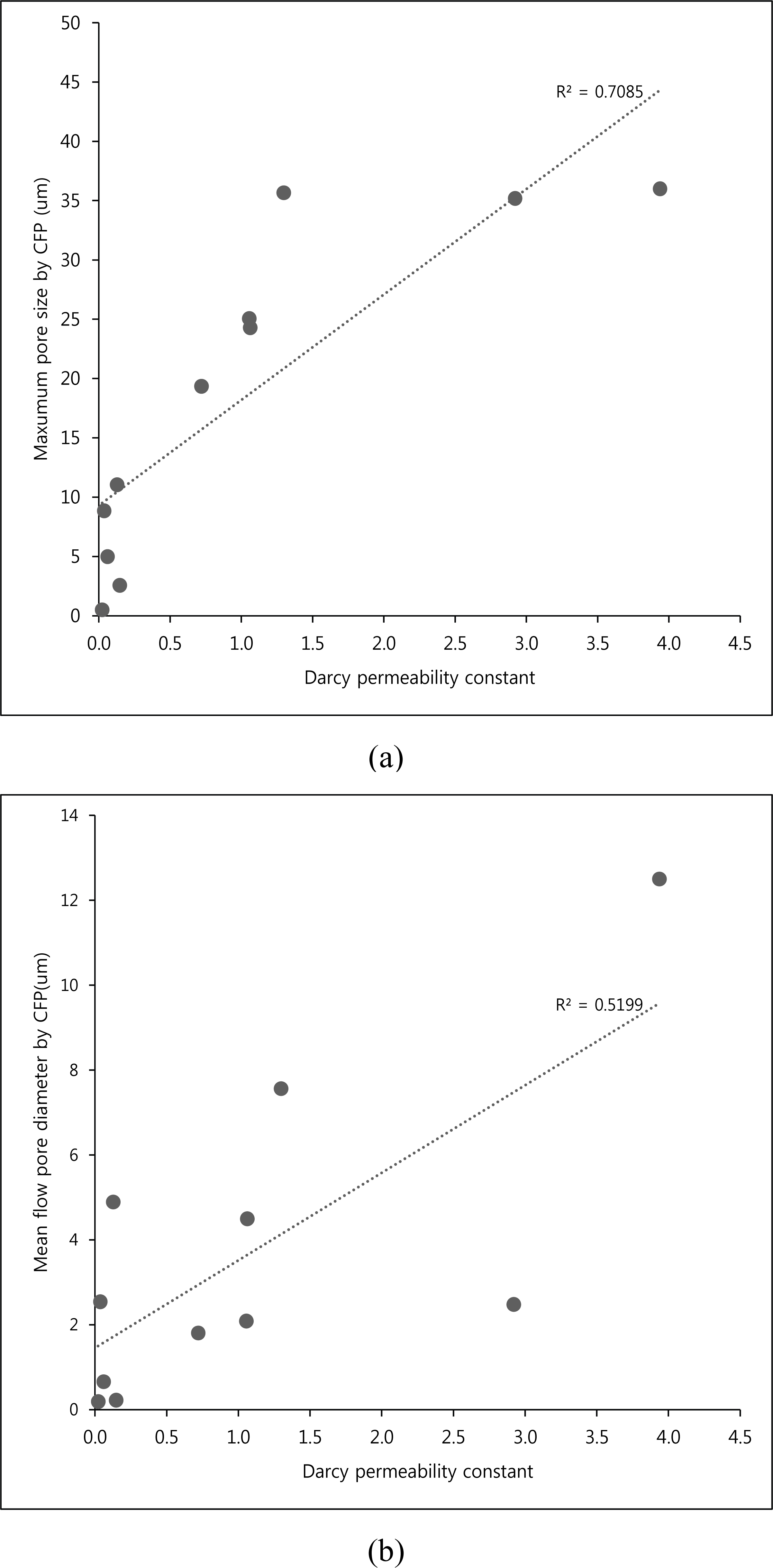
This could be understood that due to MIP including the blind pores, there is no relationship between the porosity, the pore size and gas permeability. However, in case of CFP, there is a proportional relationship between the pore size and gas permeability as shown in Fig. 9, because the method selectively measured only through pore.
4. CONCLUSION
The typical methods of MIP and the CFP were used to evaluate the pore size of wood in this study, the results of this study were as follows:
MIP could measure all pore of the wood except for closed vessels due to tylosis, but could not selectively measure specific pore element.
CFP could selectively measure the constricted part of the through pore of longitudinal direction of wood.
The wood has various micro-pore structures of in longitudinal direction as well as in radial direction, and there are blind pore-shaped microporous structure such as, cut cell lumens, the MIP measures all of these micro-pores, thus, the pore size measured by MIP tended to be smaller than the pore size measured by CFP. This indicates that the wood has a different pore structure from other porous materials.
The three types of pore defined in IUPAC are through pore, blind pore and closed pore. Only through pore can flow fluid through and CFP selectively measures through pore. Therefore, the Darcy permeability in the wood cross-section are proportional to pore size measured by CFP, and it can be predicted that the constricted part of pore size of the through pore is large if the Darcy permeability of the wood is large.





