1. INTRODUCTION
Approximately 63% of South Korea is under forest cover, the growing stock accumulation exceed the average of OECD countries (Korea Forest Service, 2016). Thus the necessity of wood use is increased, and extending the use and technical development of wood are required.
The creep behaviors of wood and wood-based materials have been studied for solid woods (Schniewind, 1968; Aratake et al., 2002), glulam (Fushitani and Bono, 1975; Hoyle et al., 1994), and various wood-based boards (Okuma and Tashiro, 1968; Bryan and Schniewind, 1965; Saito et al., 1980; Moslemi, 1964). In recent years, there is a growing interest in CLT which can be widely used in flooring, walls and ceilings owing to significantly reducing the anisotropy of woods by cross-laminating. Therefore, various researches for mechanical properties have been conducted such as the bending properties (Gülzow et al., 2011; Stelger et al., 2012; Goto et al., 2014), the shear properties (Okabe et al., 2014; Nakashima et al., 2014), the compressive properties (Ido et al., 2014) and the torsion properties (Sebera et al., 2015) and for the connection such as typical metal and screwed connectors (Gavric et al., 2014; 2015). However, the researches on creep behaviors of CLT recognize its importance, but the accumulation of the research is very small, and the research is expected to be activated. In the previous report (Park et al., 2016), with a view to effectively use small- and medium- diameter Korean wood as structural materials, cross-laminated woods were manufactured using six species of Korean softwoods and hardwoods, and static bending strength performances were investigated. As a results, the bending strength performances increased with the densities of wood species, and the anisotropy was markedly reduced by cross-laminating, and the bending strength performances perpendicular to the grain markedly improved. Also, the ratios of the measured values to the estimated values were almost similar in the cross-laminated woods with perpendicular-direction laminae in the faces, but it was very great in the cross-laminated woods with parallel-direction laminae in the faces. This was considered due to the effects of deflection caused by shear forces as the results of various cross-laminated woods manufactured with several wood species studied for many years by the authors (Park et al., 2001, 2002, 2003, 2006, 2009; Park and Fushitani, 2006, 2014). It was found that the extent of the influence was greater in softwoods with a low shear modulus than in hardwoods.
In this study, in addition to the previous study, 24 types of parallel- and cross-laminated woods were manufactured using six Korean domestic woods, and bending creep test was performed, and the influence of wood species on creep property was investigated.
2. MATERIALS and METHODS
Six species of Korean domestic woods were selected for this study. They included three softwoods: Japanese cedar, Japanese cypress and Japanese larch; three hardwoods: chestnut, tulip tree and oriental oak. Longitudinal-direction laminae of 6.7 (T) × 20 (R) × 360 (L) mm whose long axes were parallel to the grain were made with six species. And perpendicular-direction laminae were made as follows. First, longitudinal elements of 7.5 (T) × 20 (R) × 180 (L) mm parallel to the grain were made from six species and the 18 elements of them were side-jointed in the square frame. And 30 rectangular plates of 7.5 (T) × 360 (R) × 180 (L) mm were manufactured from each species, and then the plates were cut to 20 mm size in width direction and perpendicular-direction laminae of 6.7 (T) × 360 (R) × 20 (L) mm were made with long axes perpendicular to the grain. The annual ring angles of both laminae were 90°. An isocyanate type adhesive (MPU-500, Okong Co. Ltd.) formulated for a room temperature cure was used, and the amount of spread was 300 g/m2. The three-ply laminae were pressed under pressure of 0.34 MPa for 24 hours at 20°C and 65%RH. Fig. 1 shows three-ply parallel- and cross-laminated wood specimens tested. P‖ type (P‖(S), P‖(H), P‖ (L), P‖(C), P‖(T) and P‖(O), where S: Japanese cedar, H: Japanese cypress, L: Japanese larch, C: Chestnut, T: Tulip tree, O: Oriental oak) and P⊥ type (P⊥(S), P⊥(H), P⊥ (L), P⊥(C), P⊥(T) and P⊥(O)) were the specimens used to measure the bending creep parallel and perpendicular to the grain of parallel- laminated woods, respectively. And C‖ type (C‖(S), C‖(H), C‖(L), C‖(C), C‖(T) and C‖ (O)) and C⊥ type (C⊥(S), C⊥(H), C⊥(L), C⊥ (C), C⊥(T) and C⊥(O)) were the specimens used to measure the bending creep parallel and perpendicular to the grain of the face laminae of cross-laminated woods, respectively. There were 3 of each type of specimen, for a total of 72 specimens.
Bending creep test for parallel- and cross-laminated wood specimens was conducted by four-point loading as shown in Fig. 2. The span was 300 mm, and the distance between a loading point and a supporting point was 100 mm. The stress corresponding to 25% of breaking stress obtained from static bending test was applied to each specimen. The applied stresses were the average values of four bending test specimens, and the applied stresses and its coefficient of variations (CV) are shown in Table 1. The creep test was conducted for 168 h (7 days) in a constant atmosphere maintained at 20°C and 65%RH. The deflection of the mid-span was measured with a dial gauge. Total creep compliance D(t) and creep compliance Dc(t) (total creep compliance except for initial compliance) were obtained using Eqs. (1) and (2) as follows:
where P is the applied load; l is the span; b, h are the width and depth of the beam; a is the distance between a loading point and a supporting point; and y(t) is the apparent deflection at time(t) between both supporting points and contains the deflection caused by shear force. Therefore, D(t) is the apparent total creep compliance obtained from the apparent deflection containing the deflection caused by shear force.
where D(0.008) is the creep compliance at t = 0.008 h (30 s) and called initial compliance.
3. REULTS and DISCUSSION
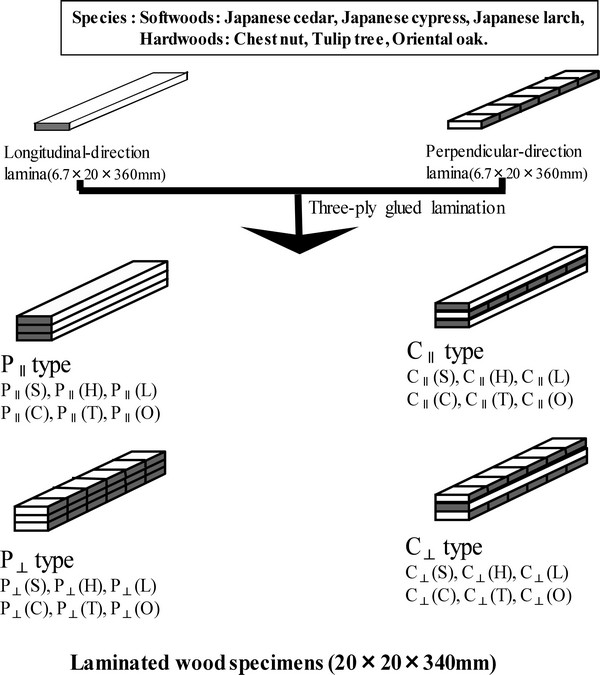
Fig. 3 shows typical examples of creep curves of parallel- and cross-laminated woods made with domestic six species. The creep curves showed the shape of the exponential function plot which markedly increased at upper right side with the increase of time, and the extent of the increase was higher in the laminated woods made with Japanese cedar with the lowest density than in that made with oriental oak with the highest density of the tested species. It was found to be higher in softwoods than in hardwoods.
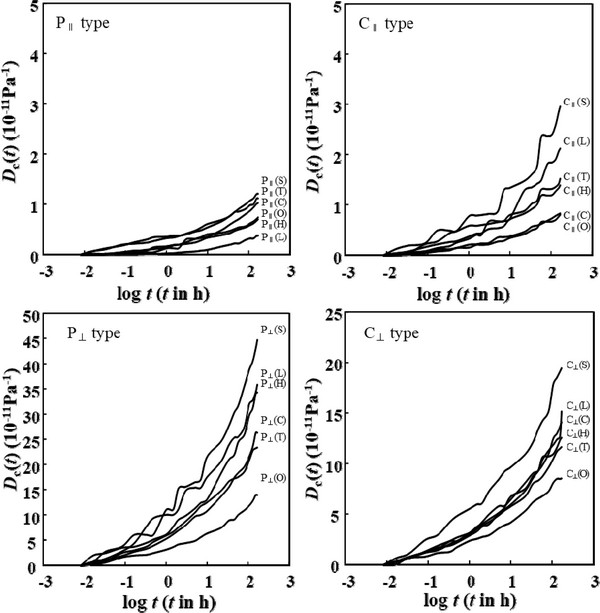
Fig. 4 shows the double logarithm plots of creep compliances and time for each type of laminated wood specimens. The creep curves showed a curvilinear behavior for about 30 minute to 1 hour after loading, but then showed a linear behavior. It has been reported in many papers that the creep curves of wood and wood-based materials were fitted to power law expressed by Eq. (3) (Schniewind, 1968; Saito et al., 1980; Arima et al., 1981; Morizumi, 1981; Hoyle et al., 1994; Aratake et al., 2002).
where, A and N are constants, and t is time.
In the logarithm regression of Eq. (3), the correlation coefficients were in the range of 0.978 - 0.998. The fitted values of N and A are shown in Table 2.
N and A are the constant values in the exponential regression between creep compliance and time [Dc(t) = AtN], D(0.008) is initial compliance (at 0.008 h), Dc(168) is creep compliance except for initial compliance at 168 h (D(168)-D(0.008)), Rc is relative creep (100(Dc(168) / D(0.008)). Each value in parentheses is the coefficient of variation (%).
The N values of P‖ type that were composed of parallel-direction laminae in all layers were in the range of 0.261 - 0.437, and P‖(H) composed of Japanese cypress had the lowest value, and had the highest value in P‖(L) composed of Japanese larch with a high coefficient of variation among the specimens. The values were in order of P‖(L) > P‖(C) > P‖(S) > P‖(O) > P‖(T) > P‖(H). It was found that there were little differences between softwoods and hardwoods. The N values of P⊥ type that were composed of perpendicular-direction laminae in all layers were in the range of 0.221 - 0.284, and P⊥(T) composed of tulip tree had the lowest value, while P⊥(C) composed of chestnut had the highest value. The values were increased with increasing density of the wood species. The values were in order of P⊥(C) > P⊥(H) > P⊥(O) > P⊥(S) > P⊥(L) > P⊥(T). It was found that there were little differences between softwoods and hardwoods. On the other hand, the N values of C‖ type cross-laminated woods that were composed of parallel-direction laminae in the faces and perpendicular-direction lamina in the core were in the range of 0.251 - 0.292, and C‖(T) composed of tulip tree had the lowest value, and had the highest value in C‖(C) composed of chestnut. The values were in order of C‖(C) > C‖(O) > C‖(H) = C‖(L) > C‖(S) > C‖(T). The cross-laminated woods made with softwoods were lower than those made with hardwoods except for that made with tulip tree. However, it was found that there were little differences by the density of species. The N values of C⊥ type cross-laminated woods that were composed of perpendicular- direction laminae in the faces and parallel- direction lamina in the core were in the range of 0.234 - 0.277, and C⊥(T) composed of tulip tree had the lowest value like C‖ type, and had the highest value in C⊥(C) composed of chestnut. The values were in order of C⊥(C) > C⊥(O) > C⊥(H) > C⊥(L) > P⊥(S) > P⊥(T). On the whole, the values were lower in those made with softwoods than in those made with hardwoods. The difference by density was not clear. These values were in a similar range as those of the cross-laminated woods that were made with Japanese cedar (Park et al., 2002; 2006) except for Japanese larch with high coefficient of variation. And these value were slightly lower than that of glulam under constant humidity condition and were considerably lower than that under humidity change. Also, these values were in a similar range as those of wood-based boards such as plywood, particle board and wood-wood based board laminated materials (Nakai, 1878; Arima, 1981; Park et al., 2010). The A values of parallel- and cross-laminated woods proportionally increased with increasing creep compliances. The values were higher in the laminated woods made with softwoods than in those made with hardwoods on the whole.
The results of creep test of parallel- and cross-laminated woods are shown in Table 2 and Initial and creep compliances of parallel- laminated woods are shown in Fig. 5.
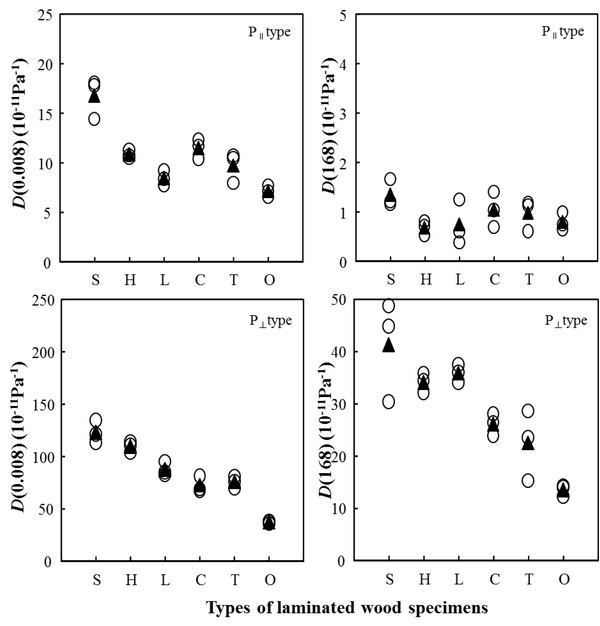
For the initial deformation of P‖ type, P‖(S) composed of Japanese cedar with the lowest density of the tested specimens had the greatest compliance, and had the lowest value in P‖(O) composed of oriental oak with the highest density of the tested specimens. The initial compliances were in order of P‖(S) > P‖(C) > P‖(H) > P‖(T) > P‖(L) > P‖(O). For the creep deformation of P‖ type, P‖(S) composed of Japanese cedar had the greatest compliance, and had the lowest value in P‖(H) composed of Japanese cypress. The creep compliances were in order of P‖(S) > P‖(C) > P‖(T) > P‖(O) > P‖(L) > P‖(H). For the initial deformation of P⊥ type, P⊥(S) composed of Japanese cedar had the greatest value, and had the lowest value in P⊥(O) composed of oriental oak. The initial compliances were in order of P⊥(S) > P⊥(H) > P⊥(L) > P⊥(T) > P⊥(C) > P⊥(O). For the creep deformation of P⊥ type, P⊥(S) composed of Japanese cedar had the greatest value, and had the lowest value in P⊥(O) composed of oriental oak. The creep compliances were in order of P⊥(S) > P⊥(L) > P⊥(H) > P⊥(C) > P⊥(T) > P⊥(O). It was found that cross-laminated woods made with softwoods were higher than those made with hardwoods on the whole, and their values showed the density dependence. The initial compliances of P⊥ type were 5.2 - 10.4 times higher than those of P‖ type, and the creep compliances of P⊥ type were 17.1 - 50.5 times higher than those of P‖ type. From these results, the creep deformation between both parallel-laminated woods was found to be considerably greater than the initial deformation. The deference was relatively great in those made with Japanese cypress and Japanese larch and was small in that made with oriental oak.
As shown in Fig. 6, for the initial deformation of C‖ type that was composed of parallel- direction laminae in the faces and perpendicular- direction lamina in the core, C‖(S) composed of Japanese cedar showed the highest initial compliance, and showed the lowest initial compliance in C‖(O) composed of oriental oak. The values were in order of C‖(S) > C‖(H) > C‖(C) > C‖(L) > C‖(T) > C‖(O). The creep compliances of C‖ type showed the highest values in C‖(S) composed of Japanese cedar and showed the lowest value in in C‖(O) composed of oriental oak like the initial deformation. The values were in order of C‖(S) > C‖(L) > C‖(H) > C‖(T) > C‖(C) > C‖(O). The initial compliance showed 1.0 - 1.3 times higher than that of P‖ type, and the creep compliance showed 1.1 - 2.6 times higher than that of P‖ type, both the initial and creep compliances were increased by cross-laminating, and the extent of the increase was found to be higher in creep deformation than in initial deformation. As shown in Fig. 5, the initial deformation of C⊥ type that were composed of perpendicular-direction laminae in the faces and parallel-direction lamina in the core showed the highest values in C⊥(S) composed of Japanese cedar, and had the lowest value in C⊥(O) composed of oriental oak. The values were in order of C⊥(S) > C⊥(H) > C⊥(C) > C⊥(L) > C⊥(T) > C⊥(O), and showed the density dependence on the whole. The creep deformation of C⊥ type showed the highest values in C⊥(S) composed of Japanese cedar, and had the lowest value in C⊥(O) composed of oriental oak. The values were in order of C⊥(S) > C⊥ (L) > C⊥(C) > C⊥(H) > C⊥(T) > C⊥(O). The initial compliance showed 0.69 - 0.87 times lower than that of P⊥ type, and the creep compliance showed 0.39 - 0.64 times lower than that of P⊥ type, both the initial and creep deformation was considerably decreased by cross-laminating, and the extent of the decrease was found to be markedly higher in creep deformation than in initial deformation.
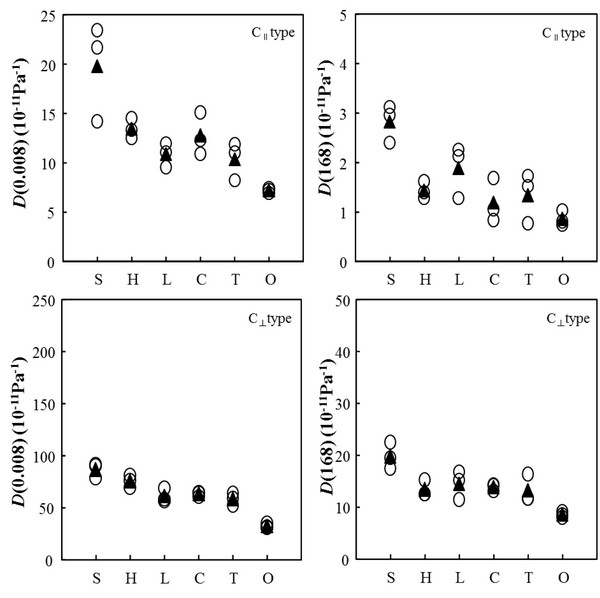
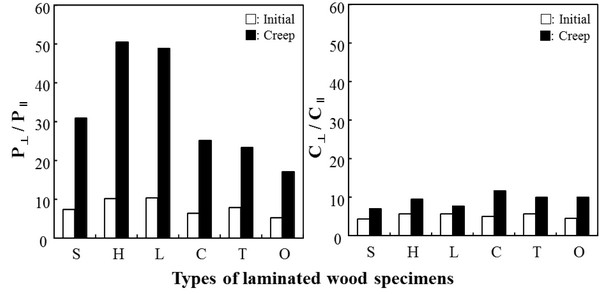
Fig. 7 shows the creep anisotropies for parallel- and cross-laminated woods. The anisotropies for the initial compliances of the cross-laminated woods were decreased to 0.54 - 0.86 times those of parallel-laminated woods by cross-laminating, and those of creep compliance were decreased to 0.28 - 0.67 times those of parallel-laminated woods by cross-laminating. The extent of the decrease was found to be much greater in creep deformation than in initial deformation.
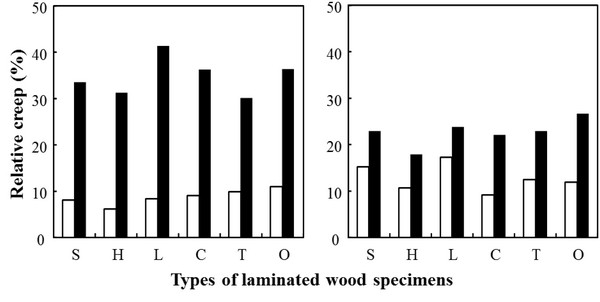
The relative creep expressed as the percentage of creep compliance to initial compliance is shown in Fig. 8. The relative creep for P‖ type showed 6.2% (P‖(H)) - 11.0% (P‖(O)). The values were in order of P‖(O) > P‖(T) > P‖(C) > P‖(L) > P‖(S) > P‖(H). The relative creep for P⊥ type showed 30.0% (P‖(T)) - 41.2% (P‖(L)). The values were in order of P⊥(L) > P⊥(O) > P⊥(C) > P⊥(S) > P⊥(H) > P⊥(T). These values showed 2.4 - 5.0 times higher than those of P‖ type. On the other hand, the relative creep of C‖ type were in the range of 9.1% (C‖(C)) - 17.2% (C‖(L)). The values were in order of C‖(L) > C‖(S) > C‖(T) > C‖(O) > C‖(H) > C‖(C), and the values were 1.5 - 1.6 times higher than those of P‖ type. The relative creep of C⊥ type were in the range of 17.8% (C⊥(H)) - 26.5% (C⊥(O)). The values were in order of C⊥(O) > C⊥(L) > C⊥(S) = C⊥(T) > C⊥(C) > C⊥(H). These values showed 0.59 - 0.64 times lower than those of P⊥ type and 1.4 - 2.2 times higher than those of C‖ type.
4. CONCLUSIONS
Cross-laminated woods were made with six domestic species, and bending creep behaviors were investigated. The conclusions obtained were as follows:
The creep curves showed the shape of exponential function plot which was sharply increased at upper right side, and the extent of the increase was higher in softwoods with low densities than in hardwoods with high densities. The creep curves showed a curvilinear behavior for about 30 minute to 1 hour after loading, but then showed a linear behavior. Therefore, it was found that the creep curves after 1 hour were able to estimate by fitting it to the power law.
The initial and creep compliances for cross-laminated woods were greatest in that made with Japanese cedar having a low density, and were lowest in that made with oriental oak having a high density.
By cross-laminating, initial and creep compliances of parallel-laminated woods (P⊥ type) composed of perpendicular-direction laminae in all layers considerably decreased, and the extent of the decrease was greater in creep deformation than in initial deformation.
The creep anisotropies expressed as ratios of creep compliance perpendicular to the grain of face laminae versus that parallel to the grain of face laminae of laminated woods were 1: 0.54-0.86 for initial deformation, and 1: 0.28-0.67 for creep deformation. By cross-laminating, the values were markedly decreased, and the extent of the decrease was found to be greater in creep deformation than in initial deformation.

