Evaluation of Bearing Strength of Self-Tapping Screws according to the Grain Direction of Domestic Pinus densiflora

LEE, In-Hwan; KIM, Keonho; SHIM, Kug-bo

doi:10.5658/WOOD.2022.50.1.1

J. Korean Wood Sci. Technol. 2022; 50(1):1-11

pISSN: 1017-0715, eISSN: 2233-7180

DOI: https://doi.org/10.5658/WOOD.2022.50.1.1

Original Article

Evaluation of Bearing Strength of Self-Tapping Screws according to the Grain Direction of Domestic Pinus densiflora

In-Hwan LEE¹, Keonho KIM¹^,^†

, Kug-bo SHIM¹

Author Information & Copyright ▼

¹Wood Engineering Division, Forest Products and Industry Department, National Institute of Forest Science, 57 Hoegi-ro, Dongdaemun-gu, Seoul 02455, Korea

^†Corresponding Author : Keonho KIM, (e-mail: keon@korea.kr)

© Copyright 2022 The Korean Society of Wood Science & Technology. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Nov 11, 2021; Revised: Dec 16, 2021; Accepted: Dec 23, 2021

Published Online: Jan 25, 2022

ABSTRACT

To evaluate the bearing strength of red pine cross-laminated timber (CLT) with self-tapping screw (STS), which is widely used as a fastener for connection in CLT building, the bearing test was conducted. Accoring to the STS’s diameters (8, 10, 12 mm), the bearing test specimens with half hole were manufactured. Bearing strength was compared and reviewed in consideration of the configuration in STS and the loading direction to the grain of red pine. As a result of the bearing test on the STS’s diameter, the yield bearing load increases as the larger diameter of the STS in all directions of the red pine. The bearing strength of the thread part (thread + tip) was higher than the shank part (shank + shank cutter). In compared with the directions to the grain of red pine, the bearing strength of the cross section parallel to the loading direction was the highest, and the tangent section was the lowest bearing strength. The average bearing strength of the loading direction in parallel to the grain was 23.43 MPa, which was about 45% higher than the average 16.16 MPa in perpendicular to the grain. The predicted bearing strength calculated by Eurocode (EN) and Korean Building Code (KBC)’s equation was lower than the experimental value. It is nessesary to propose the neuations of bearing strength reflected the configuration information of STS.

Keywords: bearing strength; cross-laminated timber (CLT); Pinus densiflora; self-tappping screw (STS)

INTRODUCTION

Joints used in wooden structures vary depending on the construction material and the required structural performance. For light frame lumber structure, mainly nail joints are used, while bolts and drift pins are generally used for heavy timber structures. Cross-Laminated Timber (CLT), a paneliged engineered wood, is at the forefront of high-value added product, and various studies are being conducted (Choi et al., 2020, 2021; Jang and Lee, 2019; Jung et al., 2020; Kang et al., 2019; Yang et al., 2021). For CLT, lag screws, self-tapping screws (STS), and ring screws were developed in consideration of the characteristics of panelized material, and the design values for products according to the structural application were presented.

STS is divided into tip, shank cutter, and thread, and each part can be inserted into the wood without drilling a hole, minimizing the wood chips and powder generated during the cutting/discharging of the STS insertion process. The angle of the STS thread and gap between the STS and lumber minimized due to the chips and wood dust not coming out from the lumber, and wood dust allowed the STS and wood to self-fasten. Due to these characteristics, STS is widely used as an important fastener for wooden buildings. In the global wooden building market, especially in European countries such as the UK and Germany, STS market share as an important wooden fastener is increasing and various studies are underway (Bedon and Fragiacomo, 2019; Dietsch and Brandner, 2015; Ringhofer et al., 2015; Sullivan et al., 2018).

The European Yield Model, based on the bearing strength of lumber and the bending characteristics of fasteners, is used for the standard allowable stress of a wooden structure joint using fasteners in the structural glued laminated timber (GLT) or CLT. The specific gravity and bearing strength of lumber show a significant correlation (Santos et al., 2010), and as an anisotropic material, lumber shows different bearing strengths depending on the grain of wood (Hwang and Komatsu, 2002). The bearing strength of CLT caused by the fastener is different than the bearing strength of laminated timber because each layer of the lumber is different.

Therefore, for CLT, the performances of the bearing strengths between fasteners and lumber in each direction must be verified.

Pinus densiflora accounts for 66.8% of Korea’s forest land with 70.35% accumulation volume of trees, making it the most important forest resource; the because of plantation is the third largest after cypress and larch (Korea Forest Service, 2020). However, in the lumber industry, the utilization rate of domestic logs is 18%, of which Pinus densiflora comprises a mere 16.6% because Pinus densiflora is mostly used as sawdust (45.1%), wood pellets (17.4%), and chips (15.9%), with 3.1% utilization rate in the lumber industry (National Institute of Forest Science, 2020). Accordingly, research is being conducted to use domestic Pinus densiflora as a structural material to increase the added value of domestic Pinus densiflora (Hong et al., 2017; Kim et al., 2013, 2015). The characteristic of the bearing strength of Pinus pinaster that is conducted based on EN383 and ASTM D5764 (Hwang and Komatsu, 2002) determined a possibility of using Pinus pinaster as structural lumber. Therefore, research on the characteristic of the directional bearing strength of Pinus densiflora that utilizes STS is necessary.

In this paper, the bearing strength performance of domestic Pinus densiflora was examined through STS as a basic study to utilize domestic Pinus densiflora as CLT.

2. MATERIALS and METHODS

2.1. Test material

As the test material, Pinus densiflora (50(T) × 50(W) × 3,600(L) mm³) with an average moisture content of 13% was prepared at a length of 50 mm and used. The fastener used for the bearing strength test was STS (Galvanized carbon steel) manufactured by Rothoblaas (Italia) (Fig. 1). According to the STS diameter (d₁), 8, 10, and 12 mm were classified into three types, and the length (L) was 120 mm. The shank diameters (d_s) were 5.8, 7, and 8 mm, while those of the shank cutter (d_c) were 6.8, 8.4, and 9 mm, larger than the shank diameter (Table 1).

Fig. 1. Shape of self-tapping screw.

Download Original Figure

Table 1. STS code and dimensions

d₁ (mm)	Code	L (mm)	b (mm)	A (mm)	d_s	d₂	d_c
8	HBS8120	120	60	60	5.8	5.4	6.8
10	HBS10120	120	60	60	7	6.4	8.4
12	HBS12120	120	80	40	8	6.8	9

A: head with drive + shank + shank cutter, b: thread + tip, STS: self-tapping screws.

Download Excel Table

2.2. Specimen production

For the bearing strength specimen, the log was quater sawn. In accordance with KS F 2156, quarter sawn lumber of 50 × 50 × 50 mm³ have a cross section (L), a radial section (R), and a tangential section (T), i.e., a specimen with a clear three-section was selected (Fig. 2).

Fig. 2. Photographs of test specimens.

Download Original Figure

When using STS, pre-hole is not required, but the groove to be fixed is machined according to KS F 2156 (2017) for the bearing strength specimen. The groove was pressed with a clamp to face the same cross section of two specimen of the same pieces, and a hole was pre-drilled with the same diameter as ds (6, 7, 8 mm) of STS in the center of the facing section. The STS(8, 10 12 mm) specimen was inserted and removed to process threaded path for bearing strength test. The bearing strength specimen was divided into two types: the bearing specimen (T-type) and the shank bearing specimen (S-type). As the thread makes a threaded path even in the bearing test specimen shank where STS is inserted, both T- and S-types have a threaded path in the groove of the bearing strength specimen. The shape of the threaded Pinus densiflora test specimen is shown in Fig. 3.

Fig. 3. Three sections of prethreaded test specimens.

Download Original Figure

The specimens were named 8T, 8S, 10T, 10S, and 12T according to the STS nominal diameter (d₁) and the area for the bearing. STS with 12 mm diameter was not included because the S part was 40 mm shorter than the specimen. A total of 150 specimen were produced by applying the STS diameter by the bearing part, the three sections of Pinus densiflora (3), and ten repetitions (10). Each type was named as shown in Table 2.

Table 2. Types of test specimen and nomenclature

	Thread (thread + tip, T)			Shank (shank + shank cutter, S)
STS diameter	8 mm	10 mm	12 mm	8 mm	10 mm
cross section	PL8T	PL10T	PL12T	PL8S	PL10S
Radial section	PR8T	PR10T	PR12T	PR8S	PR10S
Tangential section	PT8T	PT10T	PT12T	PT8S	PT10S

PL: specimen of the cross section, PR: specimen of the radial section, PT: specimen of the tangential sections.

Download Excel Table

2.3. Test methods

The Pinus densiflora specimens were subjected to humidity control in a constant temperature and humidity chamber with 65% until they reached a constant weight, the mass was measured were measured. The average annual ring width was measured based on the cross section of each specimen, and width of early and late wood were as an annual ring to calculate the average annual ring width.

Bearing strength test method was based on KS F 2156. For T-type, Pinus densiflora bearing strength was tested by inserting it into the groove so that only the thread except the tip was in contact. The S-type was tested after inserting the STS into the groove, including both the shank and shank cutter. For the prepared specimen, a compressive load was applied to a 30 ton load cell of a universal testing machine (Instron 5585) at a rate of 0.5 mm/min (Fig. 4). Compressive load and deformation were measured with Instron 5585.

Fig. 4. Configuration of bearing strength test.

Download Original Figure

3. RESULTS and DISCUSSION

3.1. Load-deformation diagram

The average specific gravity of the Pinus densiflora bearing test specimen was 0.45 ± 0.033, It is within the range of the Pinus densiflora specific gravity of studies (0.41–0.55) (Table 2, Kim, 2012; Park et al., 2006). The average annual width of the specimen was 4.44 mm, and the coefficient of variation was at 19.34%.

Fig. 5 displays the load-deformation curve of the Pinus densiflora bearing strength specimen using STS. The PL specimen (PL) cross section with fiber direction parallel loading direction parallel to the grain direction, the failure on abrupt decrease of load was clear, thus the maximum load and proportional limit could be measured. However, the specimen of the radial (PR) and tangential sections (PT), perpendicular to the grain and load directions, the load continued to increase even in the plastic stage after the elastic behavior as in the partial compression test in perpendicular to the grain. Therefore, it was impossible to measure the maximum load. The PR and PT specimen did not show splitting failure (Fig. 6). In the specimen with parallel load and the fiber directions, the proportional limit increased with the STS diameter increased.

Fig. 5. Load-deformation curves of load bearing test. PL: specimen of the cross section, PR: specimen of the radial section, PT: specimen of the tangential sections.

Download Original Figure

Fig. 6. Failure mode of tested specimens. PL: specimen of the cross section, PR: specimen of the radial section, PT: specimen of the tangential sections.

Download Original Figure

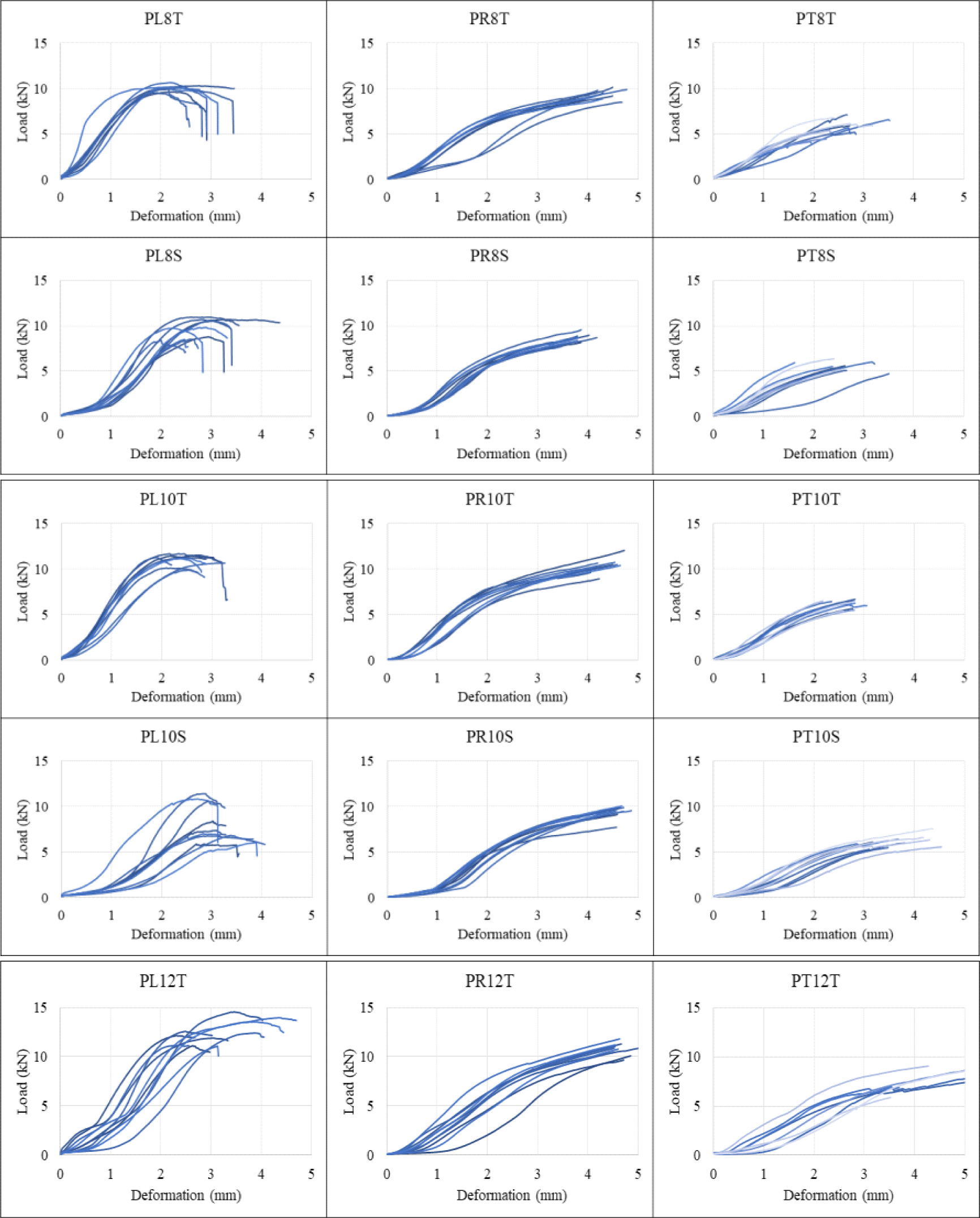
The proportional limit of the specimen (PR, PT) are as follows: For the T-type (P8T, P10T, P12T), the proportional limit increased as the diameter of the STS increased. However, for S-type (with P8S, P10S), P10S using STS with a larger diameter showed lower proportional limit than P8S attributing to the failure configuration. The proportional limit value of T-type is higher than that of the S-type (Table 3).

Table 3. STS load bearing properties of red pine

Specimen		Specific gravity (g/cm³)	Annual ring width (mm)	PL P_p¹⁾ (kN)	PR P_p (kN)	PT P_p (kN)
8T	Mean	0.45	3.99	7.42	4.86	3.31
	SD	0.02	0.89	0.32	0.41	0.75
	CV(%)	4.34	22.39	4.35	8.35	22.77
8S	Mean	0.47	4.49	6.87	4.49	3.40
	SD	0.04	0.75	0.8	0.45	0.66
	CV(%)	9.12	16.68	11.62	9.96	19.29
10T	Mean	0.43	4.39	8.28	5.09	3.50
	SD	0.03	0.93	0.37	0.57	0.42
	CV(%)	5.82	21.27	4.46	11.29	11.91
10S	Mean	0.47	5.12	7.11	4.23	3.42
	SD	0.03	0.61	1.69	0.69	0.26
	CV(%)	6.80	11.88	23.75	16.38	7.68
12T	Mean	0.43	4.20	9.54	6.32	4.46
	SD	0.01	0.77	0.75	0.67	0.93
	CV(%)	1.97	18.45	7.91	10.62	20.94
Mean		0.45	4.44	7.84	5.00	3.62
SD		0.03	0.86	1.35	0.91	0.76
CV²⁾		0.07	0.19	0.17	0.18	0.21

¹⁾ P_p: Bearing load at proportional limit.

²⁾ CV: SD/mean.

PL: specimen of the cross section, PR: specimen of the radial section, PT: specimen of the tangential sections, SD: standard deviation.

Download Excel Table

3.2. 5% offset bearing strength of Pinus densiflora lumber

The yield load value of the bearing strength specimen was calculated in accordance with KS F 2156 as shown in Fig. 7. The bearing strength was calculated by dividing the 5% offset bearing load by the projected area of the part where the STS was pressed on the lumber specimen.

Fig. 7. Load-deformation curve of 5% offset bearing strength. ① Draw a straight line representing the initial linear region of the load-deformation curve. ② By moving the straight line ① in the right direction of the horizontal axis by 5% of the STS diameter, the load at the intersection of the load-deformation curve was calculated as the 5% offset bearing strength, i.e., the similar yield load.

Download Original Figure

B T = P y / (a × d), B S = P y / {(a s d s + a c d c)}

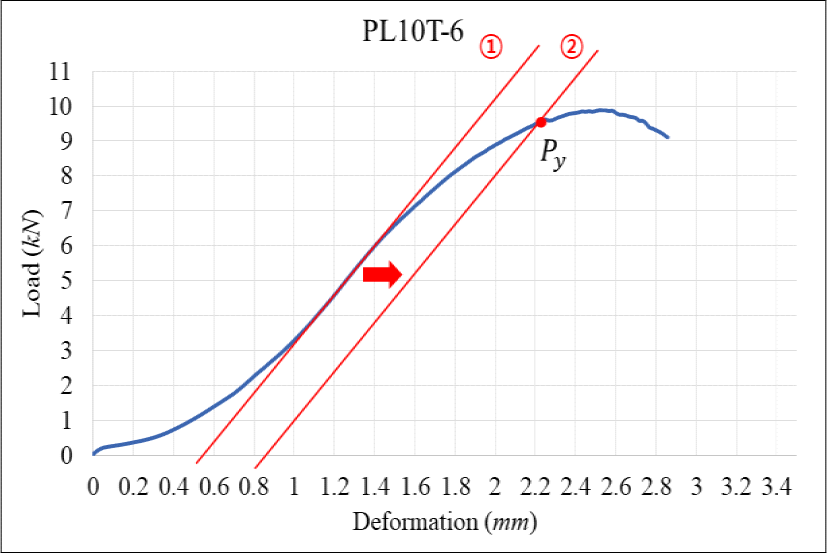
B_T: STS thread partial bearing strength

P_y: Pseudo Yield Load

a: length of specimen

d: STS thread diameter

B_S: STS shank + shank cutter partial bearing strength

a_s: STS shank length

d_s: STS shank diameter

a_c: STS shank cutter length

d_c: STS shank cutter diameter

Table 4 shows the average yield load and the bearing strength of Pinus densiflora lumber using STS. The yield load was the highest (PL12T) that pressed the cross section of 12-mm STS T-type at 11.85 kN, and the specimen (PT8S) that pressed the tangential section of 8-mm S-type was the lowest at 4.75 kN. Most of the T- (8T, 10T, and 12T) and S-types (8S and 10S) showed a tendency to increase in yield strength as the diameter increased. However, for the PL specimen with parallel fiber and load directions, the yield load of the 10S specimen was lower than that of the 8S specimen, a opposite trend to that of the maximum load value. The S-type maximum load of the 8SPL specimen was higher 10PL due to high stiffness in the fiber direction. However, the yield load showen different result due to load concentration the shank cutter mainly because of larger diameter of shank cutter (Fig. 8).

Table 4. Average offset yield load and bearing strength of Pinus densiflora measured by using STS

Specimen	Py (kN)			Bearing strength (MPa)
Specimen	L	R	T	L (F_‖)	R	T	F_⊥	F_⊥/F_‖
8T	9.88	6.90	5.11	24.71	17.25	12.78	15.01	0.61
8S	9.05	7.08	4.75	31.22	24.41	16.36	19.71	0.65
10T	10.58	8.15	5.81	21.17	16.30	11.62	13.96	0.66
10S	7.76	7.75	5.66	22.18	22.15	16.18	18.43	0.86
12T	11.85	9.53	6.90	19.74	15.88	11.50	13.69	0.69
Mean	9.82	7.88	5.65	23.8	19.2	13.69	16.16	0.69

Download Excel Table

Fig. 8. Failure mode of S-type tested specimens.

Download Original Figure

The bearing strength of all specimens decreased as the diameter of the STS increased due to the increased projected area, and the bearing strength of the S-type test specimen was higher than that of the T-type, possibly because the shank diameters (5.8, 7, 8 mm) were smaller than those of the STS thread (8, 10, 12 mm). The yield load and bearing strength in each direction of Pinus densiflora showed high values in the following order, cross section > radial section > tangential section.

3.3. Comparison between measured and calculated bearing strength of Pinus densiflora

Table 4 shows the bearing strength ratio of the R and T directions according to the fiber direction of Pinus densiflora. Except for the cleavage failure (10S) specimen, the bearing strength ratio of parallel to perpendicular to the grain was measured from 0.61 to 0.69.

In National Design Specification (NDS), the North American wooden structure standard, included in 2018. Suggesting that the CLT bearing strength can be calculated as the effective bearing length which reflects strength ratio of lamina of CLT by grain direction.

Therefore, the STS bearing strength of Pinus densiflora structural engineering wood for each load direction versus the fiber direction will act as an important factor for the prediction of Pinus densiflora CLT bearing strength. In the Korean Design Standard (KDS), the lumber bearing strength prediction formula was load direction grain suggested according to the fastener type and to the fiber direction. Eurocode 5 applies the prediction formula obtained through experiments focusing on the native species. For the STS fasteners, bearing strength prediction formulas have not yet been proposed in the international standards. Therefore, in this paper, to predict the STS bearing strength for each grain direction of Pinus densiflora, a similar lag screw bearing strength prediction formula (KDS and Eurocode 5) was applied and analyzed (Table 5).

Table 5. Bearing strength of experimental and calculated value according to grain direction

Specimen	F_‖(MPa)	KDS (MPa)	EN (MPa)	KDS/F_‖	EN/F_‖
8T	24.71	35.42	33.82	1.43	1.37
8S	30.18	36.92	35.26	1.22	1.17
10T	21.17	34.28	32.02	1.62	1.51
10S	21.33	37.52	35.05	1.76	1.64
12T	19.74	33.67	30.76	1.71	1.56

Specimen	F_⊥(MPa)	KDS (MPa)	EN (MPa)	KDS/F_⊥	EN/F_⊥
8T	15.01	23.86	23.01	1.59	1.53
8S	19.71	25.35	23.98	1.29	1.22
10T	13.96	20.36	21.35	1.46	1.53
10S	18.43	23.20	23.37	1.26	1.27
12T	13.69	18.11	20.10	1.32	1.47

KDS, Korean design standard.

Download Excel Table

KDS (NDS):

F e | | = 79 G, F e ⊥ = 216 G 1.45 d

Eurocode 5:

F e | | = 0.082 (1 − 0.01 d) ρ, F e ⊥ = 0.082 (1 − 0.01 d) ρ 1.35 + 0.015 d

F_e: bearing strength (N/mm²)

G: specific gravity (–)

d: fastener diameter (mm)

ρ: average density (N/mm³)

The predicted results of the bearing strength of KDS and Eurocode 5 were similar, but there was a difference between the measured bearing strengths and the predicted ones (Fig. 9). For the perpendicular load of grain direction, the measured strength values of the 8T, 10T, and 12T specimen were 53%, 53%, and 47%, It lower than the EN predicted values, and the 8S and 10S were measured 22% and 27% lower, respectively. A similar trend was also observed in the parallel load to grain direction (F_e‖), The results possibly resulting from applying the d₁ diameter to the formula, although the difference in the d₁ and d₂ diameters of the STS thread was larger than that of a general lag screw with a wide spacing between the threads. Because the shank had a similar diameter as the lag screw, the difference was relatively small, but the predicted value was low because the failure was concentrated in the shank cutter. The prediction formula of KDS and EN is the method of calculating the bearing strength based on the maximum load, and KS F 2156 is the method of calculating the bearing strength based on the 5% offset yield load, thus the possibility of a difference is high as well.

Fig. 9. Comparison between experimental and calculated bearing strength KDS and EN.

Download Original Figure

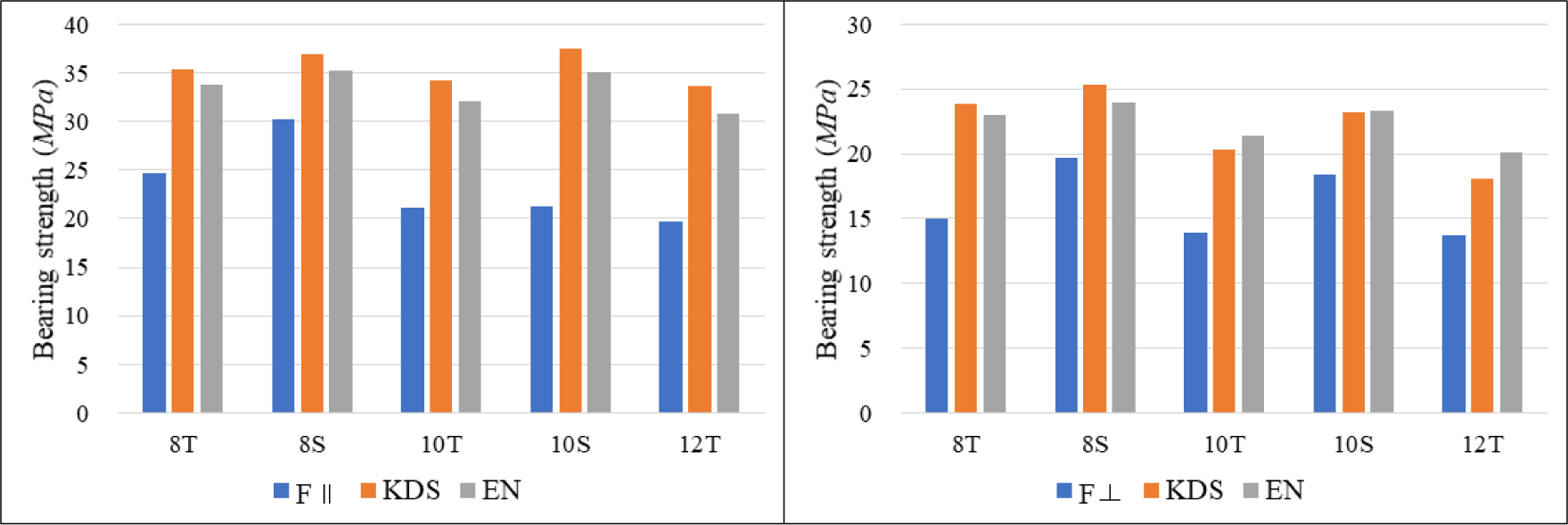
Due to the structural difference between the lag screw and STS, the empirical coefficient applied to the lag screw may not be applied to the STS. In the future, when diameters d₁ and d₂ of the thread and the coefficients of shank and shank cutter are applied, and the bearing strength for STS is calculated with the lumbers of various specific gravity to determine the appropriate empirical coefficient, a prediction formula for STS can be proposed. Our research team aims to derive a suitable empirical formula by calculating the bearing strength of STS for various species in the future.

4. CONCLUSION

In this study, STS was used to calculate the bearing strength for each load direction according to the grain direction of domestic Pinus densiflora. STS was 8, 10, and 12 mm in diameter, and the larger the diameter, the higher the yield load value in all grain directions of Pinus densiflora. The part with STS threads showed 11% lower strength value than the part without threads. As for the bearing strength of each direction of Pinus densiflora, the PL specimen parallel to the load and grain directions showed the best bearing strength, and the tangential section showed the lowest bearing strength. The bearing strength of the radial section was 19.3% lower than that of the cross section, and the bearing strength of the tangential section was 42% lower than that of the cross section. The strength ratio for each direction was calculated as 0.7 based on the specimen with parallel grain and load directions. The lumber bearing strength prediction formula using a lag screw was not suitable for STS bearing strength prediction. If an empirical formula is derived by calculating the bearing strength using tree species of various specific gravity in the future, the bearing strength prediction formula using STS according to the specific gravity can be proposed.

CONFLICT of INTEREST

No potential conflict of interest relevant to this article was reported.

ACKNOWLEDGMENT

Not applicable.

REFERENCES

Bedon, C., Fragiacomo, M. 2019. Numerical analysis of timber-to-timber joints and composite beams with inclined self-tapping screws. Composite Structures 207: 13-28.

British Standards Institution. EN 1995-1-2:2004: Eurocode 5: Design of Timber Structures - Part 1-2: General - Structural Fire Design. British Standards Institution, London, UK.

Choi, G.W., Yang, S.M., Lee, H.J., Kim, J.H., Choi, K.H., Kang, S.G. 2020. A study on the block shear strength according to the layer composition of and adhesive type of Ply-lam CLT. Journal of the Korean Wood Science and Technology 48(6): 791-806.

Choi, G.W., Yang, S.M., Lee, H.J., Kim, J.H., Choi, K.H., Kang, S.G. 2021. Evaluation of flexural performance according to the plywood bonding method of Ply-lam CLT. Journal of the Korean Wood Science and Technology 49(2): 107-121.

Dietsch, P., Brandner, R. 2015. Self-tapping screws and threaded rods as reinforcement for structural timber elements: A state-of-the-art report. Construction and Building Materials 97: 78-89.

Hong, M.K., Park, B.D., Kim, K.H., Shim, K. 2017. Performance of melamine-urea-formaldehyde resin adhesives at various melamine contents for bonding glued laminated timber under high frequency heating. Journal of the Korean Wood Science and Technology 45(4): 409-418.

Hwang, K., Komatsu, K. 2002. Bearing properties of engineered wood products I: Effects of dowel diameter and loading direction. Journal of Wood Science 48(4): 295-301.

Jang, S.S., Lee, H.W. 2019. Lateral resistance of CLT wall panels composed of square timber larch core and plywood cross bands. Journal of the Korean Wood Science and Technology 47(5): 547-556.

Jung, H., Song, Y., Hong, S. 2020. Effect of glass fiber-reinforced connection on the horizontal shear strength of CLT walls. Journal of the Korean Wood Science and Technology 48(5): 685-695.

10.

Kang, C.W., Jang, S.S., Kang, H.Y., Li, C. 2019. Sound absorption rate and sound transmission loss of CLT wall panels composed of larch square timber core and plywood cross band. Journal of the Korean Wood Science and Technology 47(1): 33-39.

11.

Kim, G.C. 2012. Study on the change of physical and anatomical properties in the pine wood by accelerated weathering test. Journal of the Korea Furniture Society 23(3): 324-331.

12.

Kim, H.K., Oh, J.K., Jeong, G.Y., Yeo, H.M., Lee, J.J. 2013. Shear performance of PUR adhesive in cross laminating of red pine. Journal of the Korean Wood Science and Technology 41(2): 158-163.

13.

Kim, K.H., Kim, S.J., Yang, S.Y., Yeo, H., Eom, C.D., Shim, K. 2015. Bonding performance of adhesives with lamina in structural glulam manufactured by high frequency heating system. Journal of the Korean Wood Science and Technology 43(5): 682-690.

14.

Korea Forest Service. 2020. Statistical Yearbook of Forestry. Korea Forest Service, Daejeon, Korea.

15.

Korean Construction Standard Center. 2018. KDS 41 33 05:2018: Design of the timber construction joint. Korea Construction Standards Center, Seoul, Korea.

16.

Korean Standards Association. 2017. KSF 2156: Method of Dowel-Bearing Strength Test for Wood and Wood-based Products. Korean Standards Association, Seoul, Korea.

17.

National Institute of Forest Science. 2020. Market Survey of Timber Product. National Institute of Forest Science, Seoul, Korea.

18.

Park, B.S., Park, J.H., Han, S.U. 2006. Variation of material properties of Korean red pine of superior families - tracheid length, microfibril angle, resin canal and specific gravity. Journal of Korea Forestry Energy 25(2): 9-15.

19.

Ringhofer, A., Brandner, R., Schickhofer, G. 2015. Withdrawal resistance of self-tapping screws in unidirectional and orthogonal layered timber products. Materials and Structures 48(5): 1435-1447.

20.

Santos, C.L., De Jesus, A.M.P., Morais, J.J.L., Lousada, J.L.P.C. 2010. A comparison between the EN 383 and ASTM D5764 test methods for dowel-bearing strength assessment of wood: Experimental and numerical investigations. Strain 46(2): 159-174.

21.

Sullivan, K., Miller, T.H., Gupta, R. 2018. Behavior of cross-laminated timber diaphragm connections with self-tapping screws. Engineering Structures 168: 505-524.

22.

Yang, S.M., Lee, H.H., Kang, S.G. 2021. Research trends in hybrid cross-laminated timber (CLT) to enhance the rolling shear strength of CLT. Journal of the Korean Wood Science and Technology 49(4): 336-359.