1. INTRODUCTION
With the rise of the environmental issue like global warming, timber structures have been spotlighted because of its eco-friendly effect, e.g. carbon dioxide assimilation and its sustainability. For decades, timber buildings have featured light-framed wood structures, so far. As interest in urban timber building increased, timber structures need to be designed for high-rise buildings to carry heavy load. Therefore, many engineered wood products that have larger cross section than sawn timber have been developed, e.g., Glued laminated timber (GLT), Cross-laminated timber (CLT) and many researches have been studied on how the mechanical properties of existing wood products are improved. Choi et al. (2018) investigated the flameretardant properties of CLT with EVA/Intumescent/ Nano-clay composite and the result showed that it reduced combustion of CLT in fire condition. Jung et al. (2019) investigated the glass fiber-reinforced shear connection on CLT wall. Lee et al. (2020) investigated the bonding performance of several adhesives in lumber-lumber according to its bonding surface and the position of pith. Iswanto et al. (2019) investigated the properties of sandwich particleboard composed of bamboo as surface layer and sugar palm fiber, cornstalk, sugarcane bagasse, and bamboo particle, as core layer. Lestari et al. (2018) investigated the mechanical properties of GLT made from jabon and pine using isocyanate adhesive. Pang et al. (2017) investigated shear and bending performance of CLT which is strengthened by nail and suggest equation to predict its load-carrying capacity. Parbuningrum et al. (2020) investigated the mechanical properties of laminated board which layers are composed of oil palm trunk waste. Qi et al. (2019) investigated the mechanical properties and dimension stability of bamboo fiber composite when the mold inhibitor is applied. Seo et al. (2018) investigated mechanical and physical properties of particle board and oriented strand board (OSB) made from Tullip tree (Liriodendron tulipifera L.). Suh et al. (2012) investigated the shear strength of nailed connection on plywood made from Korean pine (Pinus koraiensis) to substitute OSB with plywood. Also, many investigations on the related fasteners have been carried out (Oh et al., 2017).
To realize the large-scale tall buildings, it is needed to consider the performance of joint between building elements. In case of timber, welding is not possible like steel structure, so it should be connected with joints, e.g. nail, dowel, bolt and screw. Especially, self-tapping screw (STS) can be driven easily and has high load-carrying capacity than nail. It is easy to install and even predrilling is not required. For that reason, the use of the STS increased dramatically in tall timber buildings which are made of massive wood panels, such as CLT and laminated veneer lumber (LVL).
To promote the tall timber building in market, competitiveness needs to increase. As one of the efforts, new massive wood panels have been developed by making composite material of solid wood and wood-based panel, such as plywood, laminated board (Choi et al., 2018; Galih et al., 2020; Jang, 2019; Kang et al., 2019). These new massive wood panel might have higher competitiveness than typical CLT. Chang et al. (2017) evaluated the thermal conductivity of the hybrid cross laminated timber (HCLT) which use plywood as core by using thermal conductivity instrument. In comparison with typical CLT, the HCLT showed lower thermal conductivity. Choi et al. (2015) evaluated physical and mechanical properties of the HCLT. The test results showed the MOR value of the HCLT was higher than typical CLT. Also, the HCLT showed less expansion ratio than typical CLT in the dimensional stability test. To commercialize these new massive wood panel, the plywood and other veneer- based material need to be investigated about their mechanical properties as well as solid wood.
The thread of the STS provides stronger withdrawal resistance than nail and it enables to make more efficient connection. The withdrawal force on STS showed mainly three failure modes: (1) tensile failure of screw itself, (2) pull-through failure of wood by screw head, (3) withdrawal failure by thread (Ringhofer et al., 2015). Especially, the withdrawal failure is affected by wood species and the type of material. Many researchers have investigated the withdrawal resistance of screw on wood products. Cha (2013) evaluated withdrawal resistance of screw in particle board on face and side-face. Jang and Lee (2018) evaluated withdrawal resistance of lag screw, tapping screw and Sherpa screw on Larch and Spruce, and compared the effect of driven angle about wood fiber on withdrawal resistance (cross section, radial section, tangential section).
In Korean Building Code, there is no design methodology for the STS. To put the STS design formulation in the building code, experimental verifications on Korean wood products are required. Also, it needs to understand the behavior of the STS in laminated engineered wood, such as CLT, plywood, Ply-lam (Pang et al., 2020).
In this study, the applicability of the withdrawal design value estimation equation in National Design Specification for Wood Construction (NDS, 2018) for self-tapping screw was investigated on Korean wood products. The predicted values by the equation were compared with experimental data.
2. MATERIALS and METHODS
In NDS, withdrawal resistance estimation equation for wood screw is specified. Because STS is classified as wood screw, the equation was utilized to predict the withdrawal resistance of STS. The formula indicates that the main properties affecting the withdrawal capacity are specific gravity of wood products and outer thread diameter. In this study, we compared the measured withdrawal resistance with the predicted withdrawal resistance by NDS equation, and evaluated the applicability of the equation to Korean wood products.
NDS (2018) provides an equation for allowable withdrawal resistance of wood screw per penetrating depth as the following equation.
Where,
Wallowable,imperial= design value for withdrawal resistance per unit penetration depth (lbs/in)
G = specific gravity of wood product
D = outer thread diameter of the screw (inch)
Since reference withdrawal design value in Eq. 1 is expressed in the imperial system, it was converted to adjust SI unit as Eq. 2 shows.
Where,
Wallowable,SI= design value for allowable withdrawal resistance per unit penetration depth (N/mm)
G = specific gravity of wood product
D = outer thread diameter of the screw (mm)
The Wallowable is a design value for allowable stress design (ASD). Adjustment factors, a load duration (1.2) and a safety factor (6.0), are included in the Wallowable (McLain, 1997). Thus, the effect of adjustment factors were excluded to predict the withdrawal resistance of screw (Pmax) as shown in Eq. 3.
Where,
Pmax= withdrawal resistance from side grain (N)
1.2 = adjustment factor for short-term test
Wallowable,SI= design value for allowable withdrawal resistance per unit penetration depth (N/mm)
KS= safety factor for wood screw (6.0)
The withdrawal strength predicted by Eq. 3 was compared with maximum force measured by axial withdrawal test in this research. When the measured withdrawal resistance was higher than prediction or the difference between predicted and measured value was small, it is evaluated that the NDS equation is suitable for Korean wood products.
Three types of wood products are prepared; solid wood, CLT, plywood. Each wood product was tested for two types of STS, 8.0 mm (diameter) × 100 mm (length) and 6.5 mm × 65 mm. Thus, six groups for withdrawal test were prepared. All groups are tested more than 30 specimens.
The species of all wood specimens was Korean larch (Larix kaempferi), and its specific gravity and moisture content were measured after withdrawal test. The test specimens were 11 and 3 for solid wood and plywood, respectively and both were stored in laboratory condition before using. Although they stored in same laboratory condition, it assumed that the different process of each wood products derived difference in moisture content. Specific gravity of wood product specified in NDS can be calculated by Eq. 4 and it is shown in Table 1. The thickness of solid wood and plywood specimens were 24mm. The CLT specimens were three layers and composed of 30 mm thick solid wood. Thus, the thickness of CLT was 90 mm.
| Material | Thickness (mm) | Specific gravity1) | Moisture content (%) |
|---|---|---|---|
| Solid wood | 24 | 0.55 (0.12)2) | 13.23 |
| CLT | 90 (3ply, 30-30-30) | 0.55 (0.12)3) | 13.234) |
| Plywood | 24 | 0.67 (0.05) | 7.93 |
where,
G = specific gravity of wood product based on oven-dry weight and oven-dry volume
Woven-dry = oven-dry weight (kg)
Voven-dry = oven-dry volume (m3).
According to NDS, it is specified to use average specific gravity to predict withdrawal resistance in NDS. Also, the average specific gravity of wood products was used to predict withdrawal resistance in existing researches that compared experimental withdrawal resistance with prediction by NDS equation (Rammer et al., 2001; Taj et al., 2009).
Table 2 shows the information of screws. Two types of screws (Ø6.5×65 mm and Ø8.0×100 mm, Sherpa, Austria) were used. The penetration depth (lp) of screws in solid wood and plywood lamina was equal to the thickness of its specimen (24mm). The standard size of plywood was used in this study. To compare it with solid wood, same thickness of solid wood was used. The screws passed through the solid wood or plywood. In case of CLT, it was inserted into the CLT specimen except for approximately 30 mm from the screw head to connect a screw to the test machine. Thus, the penetration depth of Ø6.5×65 mm screw was 29.4 mm and that of Ø8.0×100 mm screw was 58.5 mm (Fig. 1).
The axial withdrawal resistance test was conducted according to KS F ISO 9087. To avoid unintended failure such as splitting, screws were driven with spacing of 8 times screw diameter to the adjacent screws and they are driven in the perpendicular direction to the grain. All of screws were loaded in tension with 10 mm/min by universal test machine (ZWICK co., Germany), and failed in 1 to 2 minutes. The withdrawal resistance was determined by maximum load (Fmax) where the failure occurred. (Fig. 2).
3. RESULTS and DISCUSSIONS
In the all withdrawal test, failure happened at wood as shown in Fig. 3. Fig. 4 shows that the distribution of withdrawal resistance of the specimens. Plywood_ D6.5 mostly showed higher withdrawal resistance than solidwood_D6.5 and CLT_D6.5, and the lower tail distribution of solid wood_D6.5 and CLT_ D6.5 was overlapped (Fig. 4(a)). It is because STS penetrated just one layer of CLT; the thickness of single layer of CLT was 30 mm, but the penetration depth of the screw was 29 mm. And the lamina used for the CLT was the same as the solid wood specimens. Thus, the withdrawal resistance of screw in CLT was determined by the properties of the single lamina and it is similar with that of solid wood.
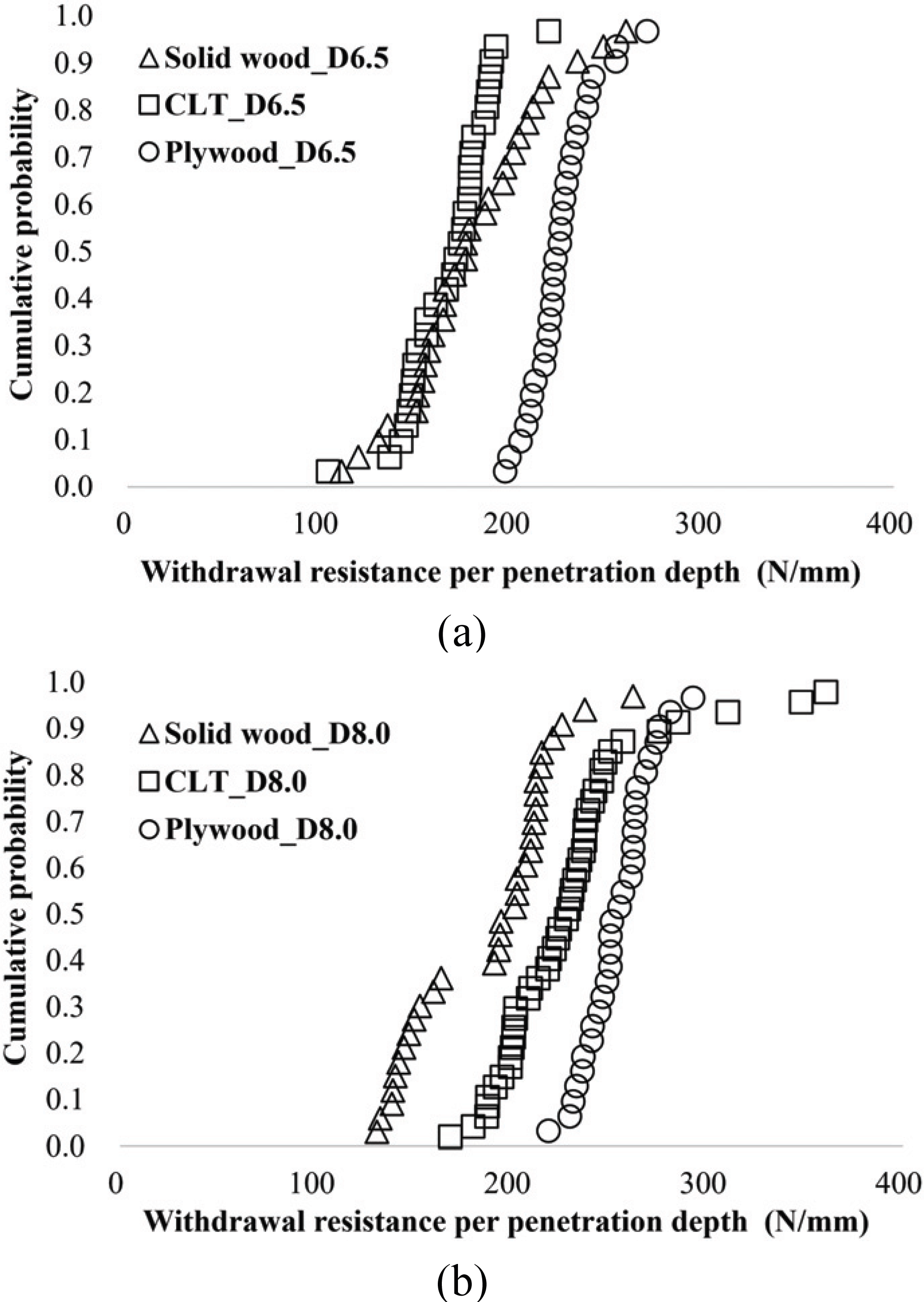
In case of screws which have 8.0mm diameter, the distribution of Plywood_D8.0 also showed higher withdrawal resistance than other wood products (Fig. 4(b)) similar with the case of 6.5mm screw. However, the lower tail distribution of Solid wood_D8.0 and CLT_D8.0 were not overlapped and the overall distribution of CLT_D8.0 showed higher withdrawal resistance than Solid wood_D8.0 unlike distribution of D6.5 (Fig. 4(a)). Since the penetration depth of the screw in CLT was 58.5 mm and two laminas of CLT were penetrated by the screw, it would be considered that the number of layers which was penetrated by the screw affected the withdrawal resistance. The effect of the number of layers in CLT has been reported by several researchers. Ringhofer et al. (2015) investigated the effect of the number of layers penetrated by the screws in CLT, supposing that withdrawal capacity of lamina products is governed by the highest stiffness layer in lamina products. And the test results showed that an increase of 7–25% in CLT (3 to 7 layers) than single layer specimens and adjustment factors for lamina products (ksys,mean, ksys,k) are suggested for the number of laminas penetrated by STS. Pang et al. (2020) investigated the withdrawal resistance of hybrid CLT (Ply-lam) and suggested the prediction model by using shear stiffness of wood products, penetration depth of screw as parameters. The research showed that the withdrawal resistance is determined by the highest shear stiffness in lamina products.
As mentioned previously, the NDS predicted the screw resistance by the average specific gravity of the wood. Since the penetration depths of the screw for each wood products were different, the average withdrawal resistance per unit length was derived (Table 3). When 8.0 screws were used, the resistance was greater than when 6.5 screws were used. The inner/ thread diameter ratios of Ø8.0×100 mm and Ø6.5×65 mm was 0.66 and 0.50, respectively. The withdrawal capacity is determined by shear stiffness of wood products, and the screw which have large inner/ thread diameter ratio can provide more withdrawal resistance because of increase in contact area (Fig. 5). The coefficient of variation (COV) decreased in the order of plywood, CLT, and solid wood specimens. This shows that the variation in specimens decreases as the number of layers increases.
The estimation equation in NDS for deriving withdrawal resistance of wood screw requires three parameters (specific gravity, outer thread diameter and penetration depth). The specific gravity is characteristic of wood products, and it has large variation depending on the wood products. Because of the variation of the specific gravity, the withdrawal resistance of wood products can also be variable. Therefore, it is quite important to determine representative specific gravity to be input on the estimation equation.
In current building code, specific gravities of solid wood for each species are specified already. For larch, 0.5 is supposed to input as the specific gravity. In case of CLT, specific gravity isn’t specified but it is reasonable to suppose that the specific gravity of CLT and solid wood are same. Because CLT is made of solid wood lamina and the glue layer cannot make large effect on its specific gravity (3ply-2 glue layers), the specific gravity must be the same as the solid wood. In contrast, specific gravity of plywood isn’t specified in current building code. So, the average specific gravity of plywood (0.67) measured in this research was used to predict withdrawal resistance. Predicted withdrawal resistances of each wood products are compared with measured withdrawal resistance to validate accuracy of estimation equation (Table 4).
As a result, the measured withdrawal resistances of CLT and solid wood were higher than prediction except for solid wood_D8.0. Considering the safety factor (6.0), the difference between prediction and measured value in solid wood_D8.0 is quite small. Hence, it is considered that the withdrawal design value estimation equation in NDS is suitable for solid wood and CLT made by Korean Larch. In contrast, the measured withdrawal resistance of plywood was lower than prediction. Because the equation was made for deriving the withdrawal resistance of solid wood, it is inaccurate for plywood.
In addition, it is assumed that the withdrawal resistance of wood products was affected by the effect the number of layers penetrated by screw. In Table 4, the measured withdrawal resistance of CLT_D8.0 was higher than that of CLT_D6.5 although the measured withdrawal resistances were divided with penetration depth of screw for each specimen. However, the effect cannot affect the plywood because it is composed of thin veneers. It assumed that the effect of penetrated layers is present when each lamina has enough withdrawal capacity. Further researches are needed to verify this assumption.
4. CONCLUSIONS
In this study, the applicability of withdrawal design value estimation equation in NDS for Korean wood products was investigated. It validated with the experimentally tested withdrawal resistance for three wood products (solid wood, CLT, plywood) made by Larix kaempferi with two types of screws (Ø6.5×65 mm, Ø8.0×100 mm). As a result, the measured withdrawal resistance of plywood is much lower than prediction. Therefore, it is considered that the withdrawal design value estimation equation in NDS is inappropriate to plywood. In contrast, it is enough to predict withdrawal resistance of solid wood and CLT because the measured withdrawal resistance was higher than prediction.
In addition, the effect of the number of penetrated layers was observed by comparing solid wood with CLT. However, it seems to be invalid if each lamina does not have withdrawal resistance. To verify this, further researches are required.












