Verifying the Possibility of Investigating Tree Ages Using Resistograph

Oh, Jung-ae; Seo, Jeong-Wook; Kim, Byung-Ro

doi:10.5658/WOOD.2019.47.1.90

2019; 47(1):90-100

pISSN: 1017-0715, eISSN: 2233-7180

DOI: https://doi.org/10.5658/WOOD.2019.47.1.90

Original Article

Verifying the Possibility of Investigating Tree Ages Using Resistograph

Jung-ae Oh², Jeong-Wook Seo³, Byung-Ro Kim³^,^†

Author Information & Copyright ▼

²Wood Products Analysis & Certification Division, Korea Forestry Promotion Institute, Seoul 07570, Republic of Korea

³Department of Wood and Paper Science, Chungbuk National University, Cheongju 28644, Republic of Korea

^†Corresponding author: Byung-Ro Kim (e-mail: brkim@cbnu.ac.kr, ORCID: 0000-0001-5800-2058)

Received: Oct 25, 2018; Accepted: Jan 03, 2019

Published Online: Jan 25, 2019

Abstract

This study aims to determine the ideal feed speed of a resistograph to evaluate the number of tree rings in several tree species. The needle speed was fixed at 1,500 r/min. Herein, various tree species, such as Pseudotsuga menziesii, Pinus koraiensis, Abies holophylla, and Zelkova serrata, were considered for experiments. Results showed that the most proper feed speed for Zelkova serrata, Larix kaempferi, Pseudotsuga menziesii, Abies holophylla, and Pinus koraiensis was 75, 100, 100, 150, and 175 cm/min, respectively. However, in all the cases, the electric resistance values of tree ring narrower than 1 mm were not suitable for determining tree-ring boundaries. Upon comparing the inter-annual time series of ring widths and electric resistance values of resistograph, a meaningful synchronization was verified. If resistograph would be improved to the extent that it can measure tree rings narrower than 1 mm, it can replace the conventional method used for counting the number of tree rings in the increment cores. Additionally, it can also be used to investigate the tree growth.

Keywords: tree age; resistograph; electric resistance values; feed and needle speeds; tree ring

1. INTRODUCTION

The conventional methods used for measuring the age of trees include the tree-ring observation method, stem node observation method, and diameter measuring method. Although tree-ring observation is the most accurate of these methods (Jeong et al., 2017; Seo et al., 2017a, b), cases wherein this method is actually used are rare. This is because scars occurring from the collection of increment cores can damage the growth and development of big old trees and can wither them. However, trees can prevent moisture evaporation and can mitigate the invasion of germs in case of scars (Shigo et al., 1977; Dujesiefken et al., 2006). Furthermore, the cambiums and oil cells around the scar create wound tissues that to cover a scar using a different mechanical and chemical characteristics than that normal cells (Grunwald et al., 2002; Frankenstein et al., 2005), which do not hinder the growth and development (Oh et al., 2017).

A resistograph was developed for measuring the inner condition of trees and the degree of decomposition of wood materials by inserting a needle into the tree and displaying the difference in the electric resistance, which were caused by the density difference of the xylem, in the form of a graph (Frank, 1994; Gruber, 2000). In countries other than Korea, resistograph is mainly used to calculate the degree of decomposition of trees (Fikret, et al., 2003; Denise, 2010; Frank, 2013) or for confirming the degree of decomposition of materials in ancient architecture (Ceraldi et al., 2001), analyzing the formation and decomposition of the callus caused by forest fires (Michael et al., 2003) or analyzing the shape of trees affected by landslides (Saez et al., 2008). In Korea, it has been verified that the materials of wooden cultural assets and wooden installations can be evaluated using resistograph (Lee et al., 2003; Hwang et al., 2008), and it is often used for a non-destructive diagnosis to analyze the degree of decomposition of wooden materials (Jung et al., 2014; Lee et al., 2014).

Studies that measured tree ages using resistograph and aimed to verify decomposition are rare. Resistograph can distinguish earlywood and latewood at the site using graphs, but due to the problems associated with the sensor that hinders distinguishing between earlywood and latewood, it is difficult to measure the ages of big old trees or trees with hard trunks (Son, 2007). However, cases of measuring tree ages using resistograph have been reported recently. Bilgin et al. (2012) verified whether resistograph can be used for measuring ages of needleleaf trees with distinct tree rings and reported that it is possible to measure ages of P. brutia. A previous study evaluated the ages by putting the relation of the diameter at breast height and the age of trees into a regression equation, and compared the result with the tree age measured by resistograph. The usefulness of resistograph was also verified in a study (Lukaszkiewicz et al., 2005). However, there are hardly any studies conducted outside Korea that used resistograph to investigate tree ages. Therefore, this study aims to measure the age of trees using a distinct boundary of tree rings with resistograph and reviewed the possibility of resistograph for estimating tree ages.

2. MATERIALS and METHODS

2.1. Materials

Disks of 5 tree species, namely Larix kaempferi, Pseudotsuga menziesii, Pinus koraiensis, Abies holophylla, and Zelkova serrata, with a distinct boundary of tree rings were prepared to determine the number of tree rings using resistograph (Table 1).

Table 1. Preliminary test to compare the number of tree rings determined by the resistograph with the number of tree rings determined by the traditional tree-ring measurement technique in dendrochronology for five different tree species

Download Excel Table

2.2. Method

2.2.1. Resistograph needle and feed speed

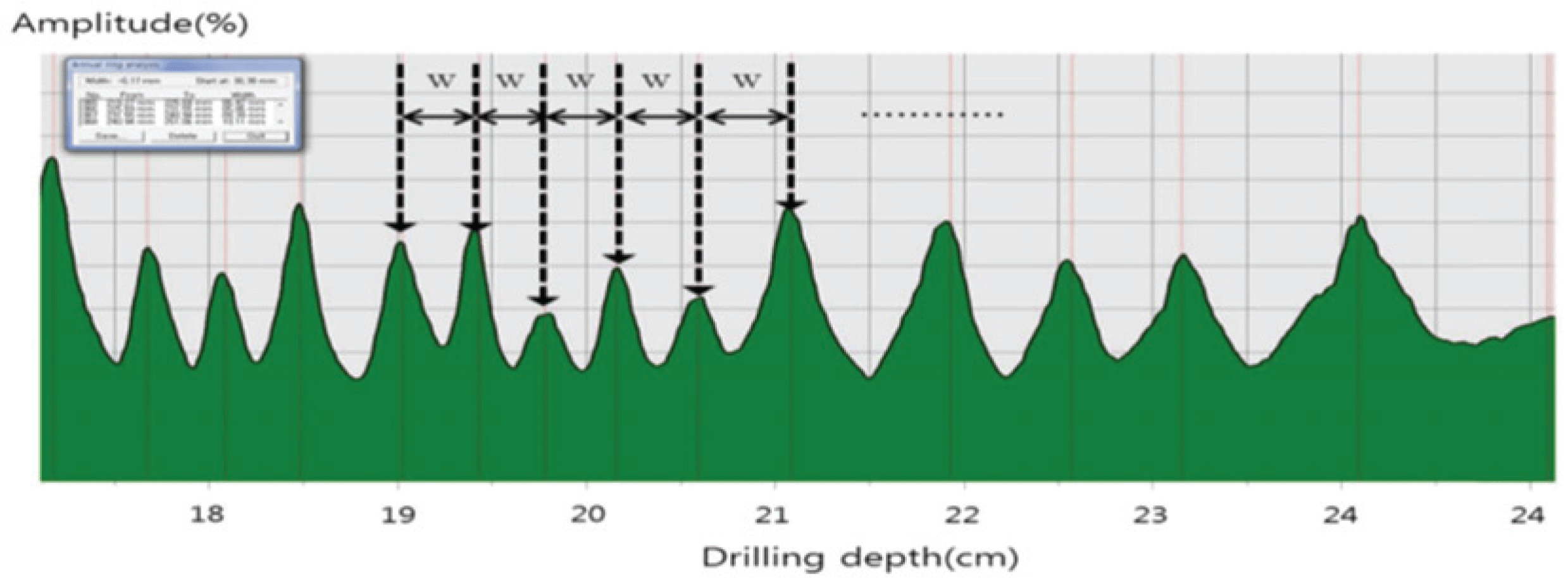
LINTAB system and resistograph were used to measure tree rings aligned in the direction to the measuring needle of resistograph (Fig. 1) is inserted. It is more stable and tree-ring boundaries are clear when the amplitudes of the graph are within the range of 40%–60% (IML Australia ⓒ, 2013). For the needle and feed speeds of resistograph, stable amplitudes based on the latewood percentage were used.

Fig. 1. Resistograph, where A is adapter sleeve, B is control unit, C is handle bar, and D is battery.

Download Original Figure

2.2.2. Comparison of tree-ring widths by LINTAB and resistograph

The tree-ring widths of graphs drawn by resistograph were digitalized (PD-tool pro, Fig. 2). The accuracy of the equipment was verified by comparing the digitalized tree-ring widths with the tree-ring width graphs measured by LINTAB.

Fig. 2. Ring-width measurement method for Pinus densiflora using PD-tool pro, where w is the tree-ring width.

Download Original Figure

3. RESULTS and DISCUSSION

3.1. Resistograph needle and feed speed

As a result of measuring tree ages using the age measurer, larch (Larix kaempferi) had 36 tree rings and 27.92% of average latewood width, douglas fir (Pseudotsuga menziesii) had 29 tree rings and 31.71% of the average latewood width, Korean pine (Pinus koraiensis) had 36 tree rings and 12.94% of the average latewood width, fir (Abies holophylla) had 32 tree rings and 14.53% of the average latewood width, and zelkova (Zelkova serrata), broadleaf trees, had 63 tree rings and 76.15% of the average latewood width (Table 2). It is reported that the stable amplitude range for analyzing tree ages using resistograph is 40%–60% (IML Australia ⓒ, 2013). To investigate the needle and feed speeds within this range, different needle and feed speeds were used based on the latewood percentage for each tree species to measure the resistance value of tree rings (Ukrainetz et al., 2010; Frank, 2012). Resultantly, the tree-ring boundaries clearly appear at 1,500 r/min of needle speed regardless of tree species (Fig. 3). Zelkova (latewood percentage: 75.07%) with a high percentage of latewood used the slowest feed speed of 75 cm/min. Larch (latewood percentage: 27.92%) and douglas fir (latewood percentage: 31.71%), which have a medium percentage of latewood, used a feed speed of 100 cm/min. Korean pine (latewood percentage: 12.94%) and fir (latewood percentage: 14.53%), which have a low percentage of latewood, used feed speeds of 150 and 175 cm/min, respectively, to verify stable amplitudes and distinct tree-ring boundaries (Table 2). Fig. 4 shows the amplitudes and distinct tree-ring boundaries of fir and zelkova.

Table 2. Results of tree-ring analysis according to the feed speed of resistograph

Species	Number of tree ring	Avg. of latewood width (%)	Feed speed (cm/min)	Needle speed (r/min)
Larch (Larix kaempferi)	36	27.92	100	1500
Douglas fir (Pseudotsuga menziesii)	29	31.71	100	1500
Korean pine (Pinus koraiensis)	36	12.94	175	1500
Fir (Abies holophylla)	32	14.53	150	1500
Zelkova (Zelkova serrata)	63	75.97	75	1500

Download Excel Table

Fig. 3. Comparing the curves with needle speeds of (A) 1500 and (B) 2000 r/min.

Download Original Figure

Fig. 4. Resistograph profile of softwood and hardwood, where A is Abies holophylla and B is Zelkova serrata.

Download Original Figure

3.2. Tree-ring widths using LINTAB and Resistograph

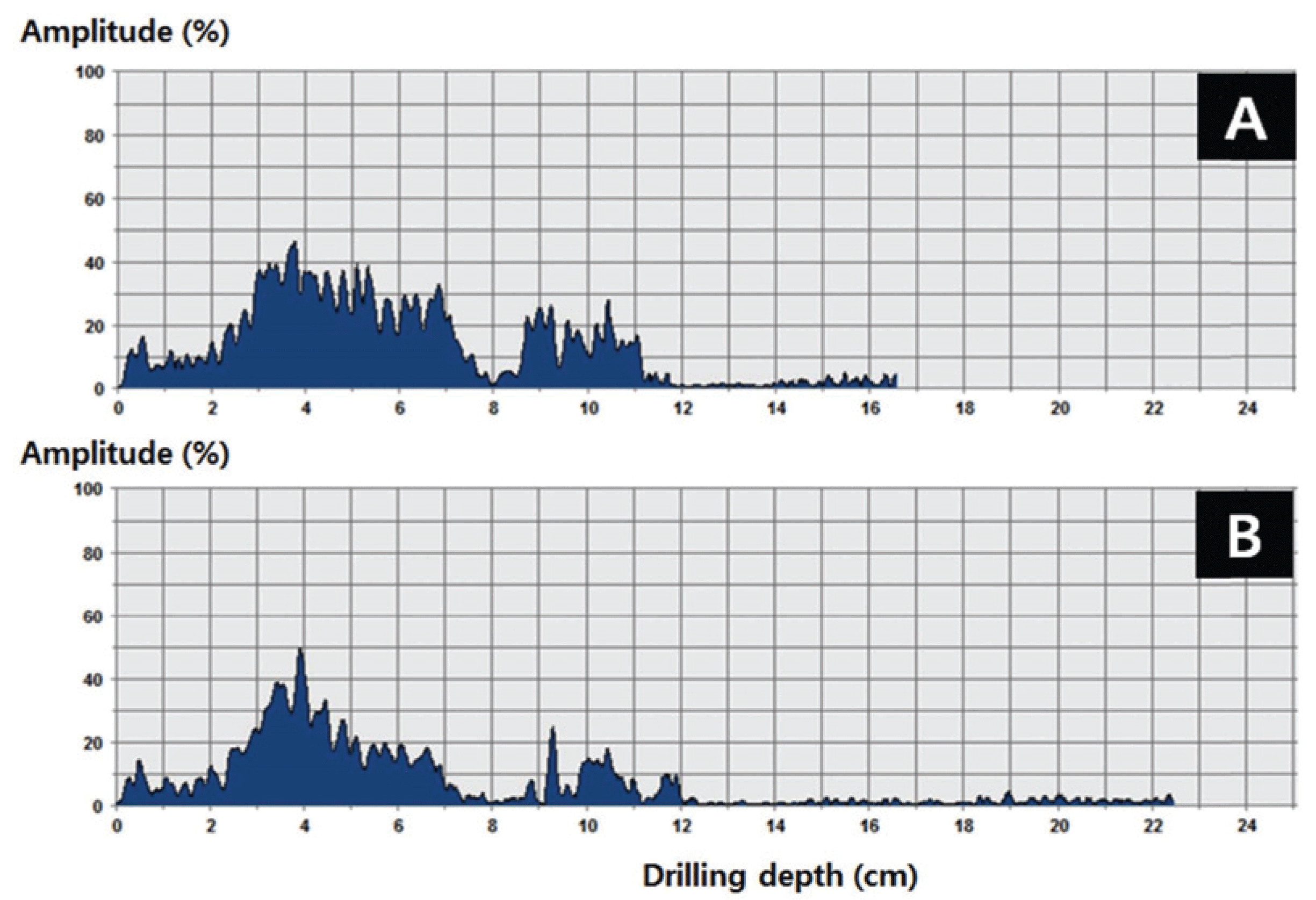
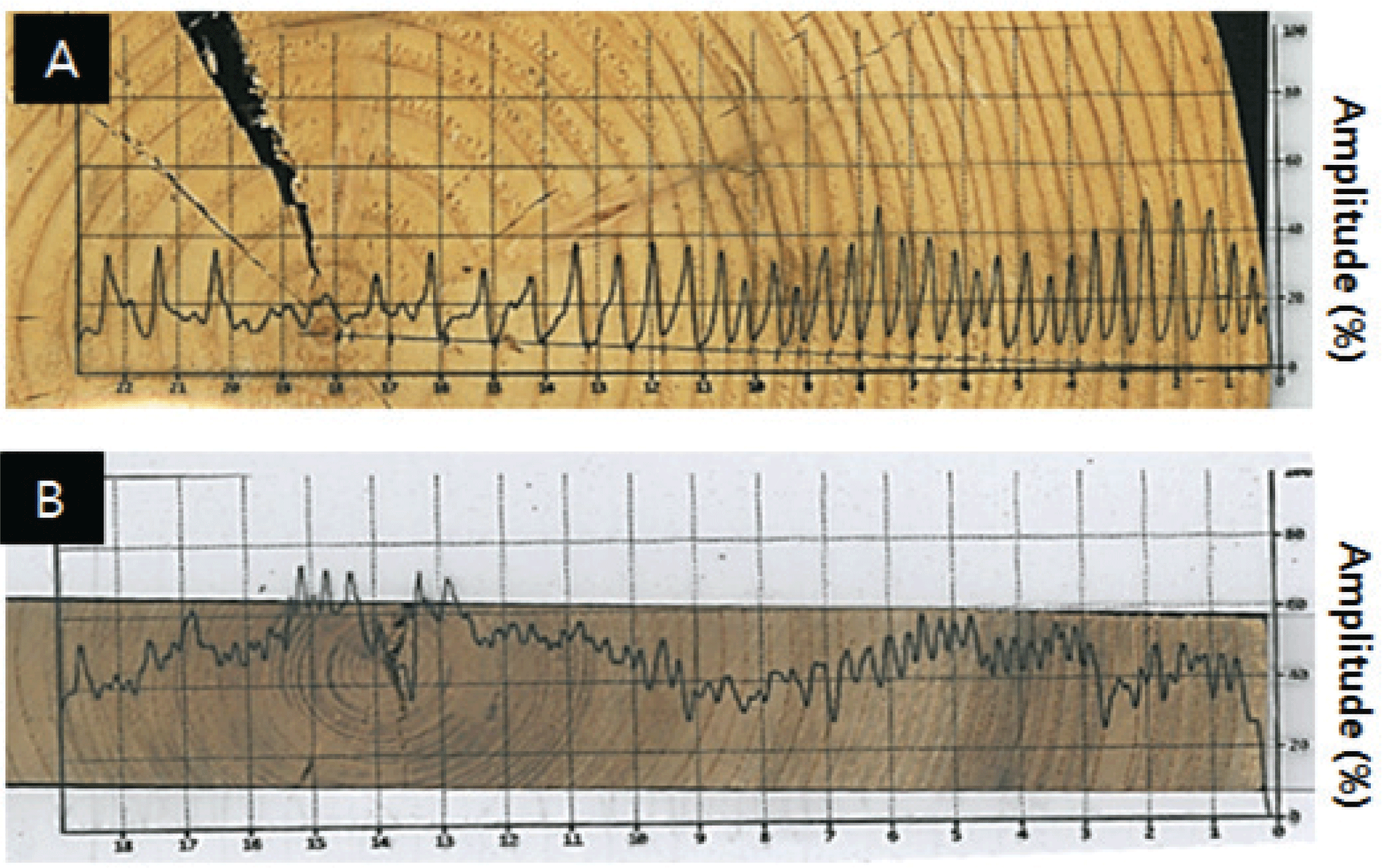
Table 3 lists the measurement results of tree-ring widths of 5 disks using LINTAB and resistograph. Upon comparing the mean tree-ring widths measured using both the methods, larch, douglas fir, and Korean pine showed the differences of 0.03, 0.08, and 0.01 mm, respectively. Fir and zelkova showed the same values. Table 4 lists the number of tree rings of 5 disks measured by LINTAB and resistograph. Except for larch which had 4 differences, all showed the same number of tree rings.

Table 3. Measurement results of tree-ring widths between the two methods

Species	Tree-ring width (mm) using the LINTAB			Tree-ring width (mm) using the resistograph
	Minimum	Mean	Maximum	Minimum	Mean	Maximum
	Larch	0.06	0.30	0.86	0.06	0.33	1.18
Douglas fir	0.20	0.62	2.51	0.22	0.54	1.03
Korean pine	0.20	0.51	0.87	0.28	0.52	0.88
Fir	0.19	0.56	1.00	0.23	0.56	1.04
Zelkova	0.06	0.21	0.51	0.03	0.21	0.46

Download Excel Table

Table 4. Differences of the number of tree rings between the two methods

Species	Number of tree-rings		Difference
	LINTAB	Resistogaraph
	Larch (Larix kaempferi)	36		32	4
Douglas fir (Pseudotsuga menziesii)	29	29	0
Korean pine (Pinus koraiensis)	36	36	0
Fir (Abies holophylla)	32	32	0
Zelkova (Zelkova serrata)	63	63	0

Download Excel Table

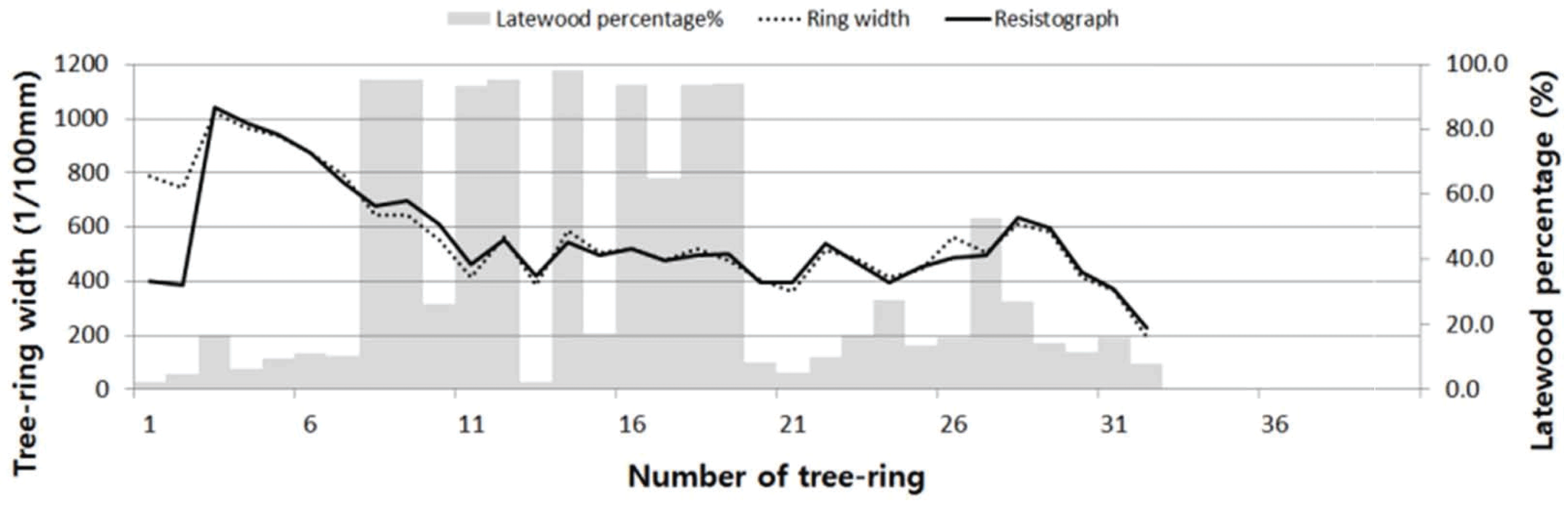
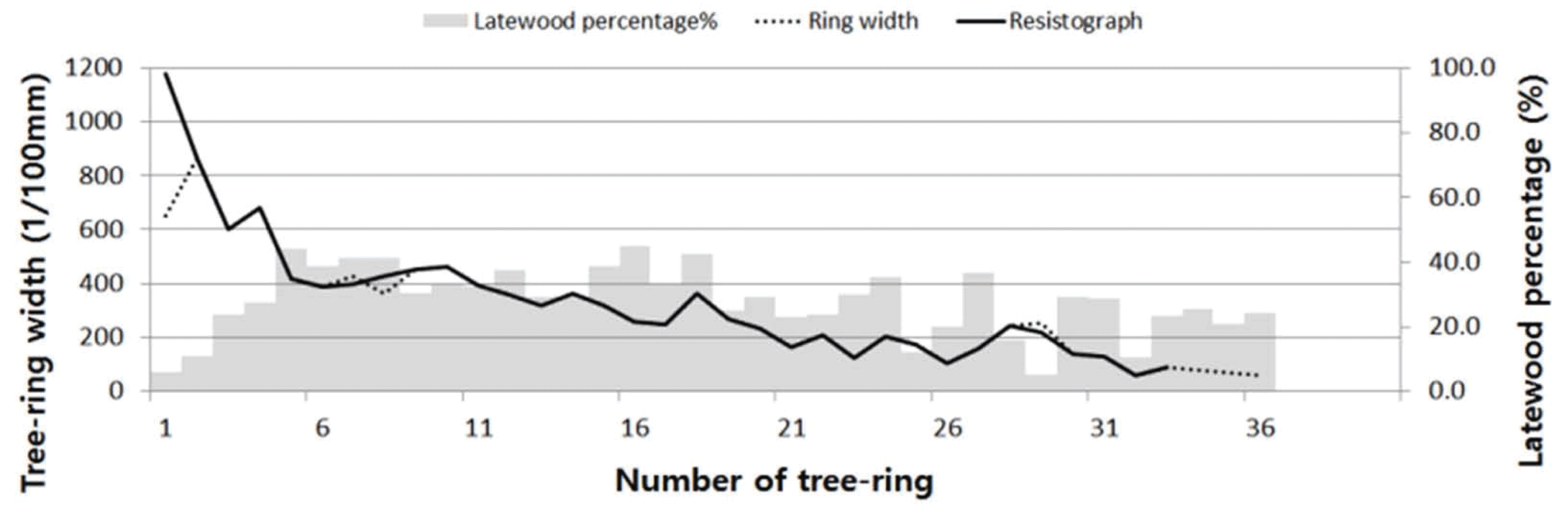
Upon comparing the 5 species with LINTAB and resistograph, all species except for zelkova had similar patterns. Fig. 5 shows the comparison of LINTAB and resistograph of fir, and they correspond approximately. In the case of zelkova, narrow tree rings were distributed on the whole regardless of heartwood and sapwood. In particular, the mean tree-ring width from the 6^th to 29^th was 0.15 mm (Fig. 6). The sapwood part of larch had the mean tree-ring width of 0.07 mm and narrow tree rings of sapwood cause the difference in the number of tree rings (Fig. 7). Therefore, it seems that the narrow tree rings bring the difference in the number of tree rings between 2 measurement methods (Eckstein et al. 1994) and it is difficult to accurately measure narrow tree rings with resistograph.

Fig. 5. Annual variations in the tree-ring widths measured by LINTAB system (dotted line) and resistograph (solid line) and the annual variations of latewood rate for Abies holophylla.

Download Original Figure

Fig. 6. Annual variations in the tree-ring widths measured by LINTAB system (dotted line) and resistograph (solid line) and the annual variations of latewood rate for Zelkova serrata.

Download Original Figure

Fig. 7. Annual variations in tree-ring widths measured by LINTAB system (dotted line) and resistograph (solid line) and the annual variations of latewood rate for Larix kaempferi.

Download Original Figure

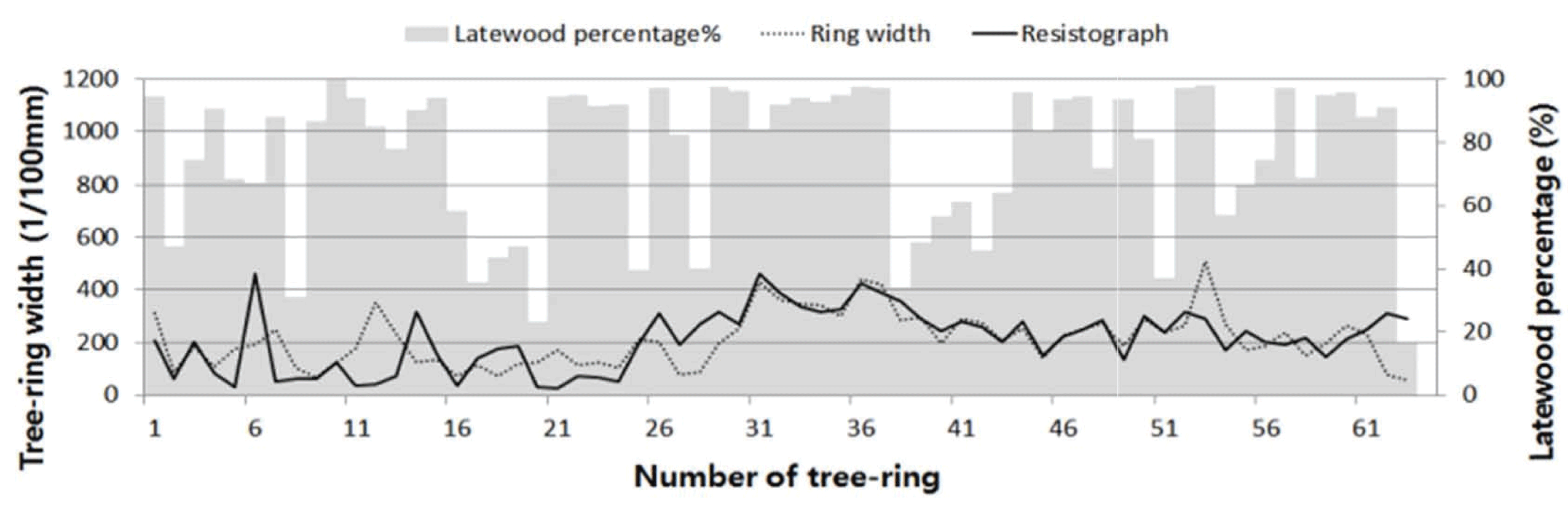
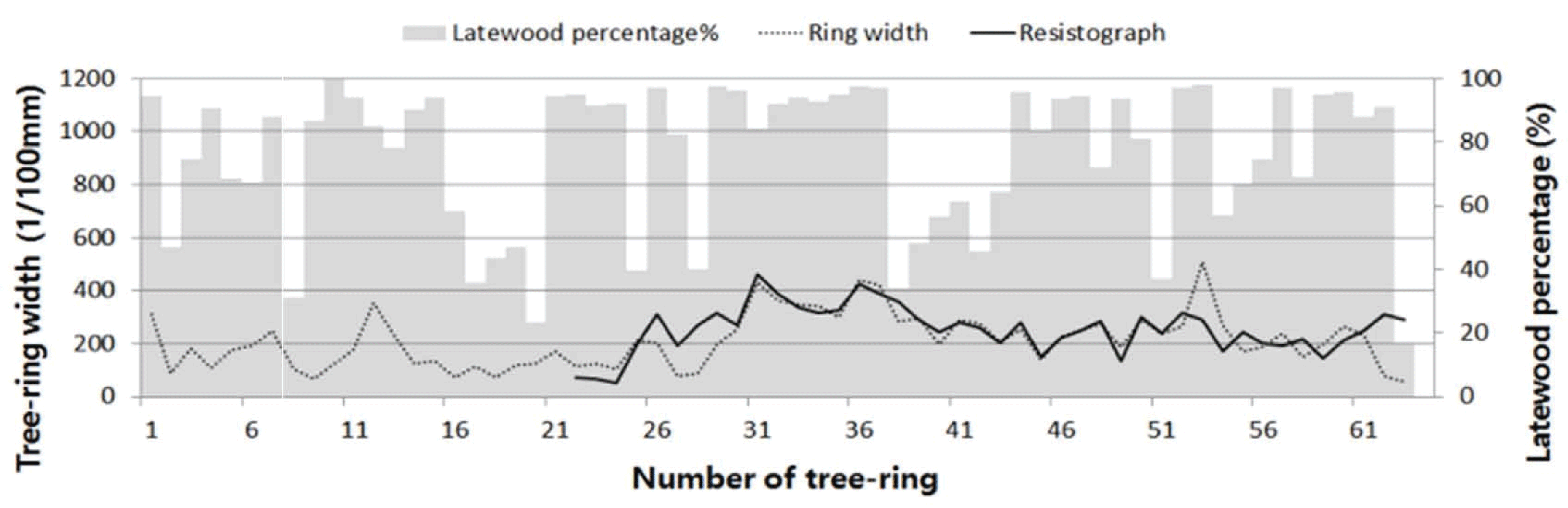
As a result of the statistical comparison, all tree species except zelkova showed statistically significant t values of over 3.5 (Table 5). In the case of zelkova, the t value was 0.8 because it was impossible to measure the accurate width of tree rings due to the tree rings being narrower than 1 mm. The Glk values for verifying the conformity of code were 91% for larch, 82% for douglas fir, 83% for Korean pine, and 92% for fir, which were statistically significant (Table 6). In the case of zelkova, the high conformity was shown except for the tree rings from 1 to 20, which are narrow rings with inconsistent cross-dating, in macroscopy (Fig. 8). It also showed statistically significant results with the t value of 4.2 (overlap period 42) and the Glk value of 68%. Thus, measuring tree ages with resistograph can be used in species with distinct tree rings with over 1 mm in width, and it is possible to measure accurate tree ages by analyzing the tree-ring width graph using resistograph and graph by cross-dating. Additionally, the tree-ring width graph of resistograph can be used to investigate the growth increment.

Table 5. t-value matrix between LINTAB and resistograph

	Larch	Douglas fir	Korean pine	Fir	Zelkova
Larch-R	10.3(33*)
Douglas fir-R		4.9(82*)
Korean pine-R			8.9(83*)
Fir-R				10(92*)
Zelkova-R					0.8(63*)

R is the resistograph measurement and * is the overlap period

Download Excel Table

Table 6. Glk matrix between LINTAB and resistograph

	Larch	Douglas fir	Korean pine	Fir	Zelkova
Larch-R	91%
Douglas fir-R		82%
Korean pine-R			83%
Fir-R				92%
Zelkova-R					60%

R: Resistograph measurement

Download Excel Table

Fig. 8. Cross-dating results after the removal of narrow rings (Zelkova serrata).

Download Original Figure

4. CONCLUSION

This study was conducted to find the most proper resistograph needle and feed speeds to investigate the number of tree rings in different tree species. Larix kaempferi, Pseudotsuga menziesii, Pinus koraiensis, Abies holophylla, and Zelkova serrata with distinctive tree-ring boundaries were used for the test. It was found that the most proper needle speed was 1,500 r/min, wherein the tree-ring boundaries appeared clearly. The most proper feed speed for Zelkova serrata, Larix kaempferi, Pseudotsuga menziesii, Abies holophylla, and Pinus koraiensis was 75, 100, 100, 150, and 175 cm/min, respectively. The LINTAB and resistograph graphs agreed as well. However, in all species, the widths of tree ring narrower than 1 mm were not suitable for determining tree-ring boundaries. If resistograph could be improved to measure tree ring narrower than 1 mm, it could displace the conventional tree-ring observation method for counting the number of tree rings in increment cores with resistograph. Additionally, tree-ring width graphs can be used to investigate the tree growth.

Appendices

APPENDIX (Korean Version)

레지스토그래피를 이용한 수령조사 가능성 검토

초록 : 본 연구는 수목의 수령을 조사하는 방법으로 레지스토그래피를 활용하는데 있어서 수종별로 가장 적합한 삽입속도를 찾기 위하여 수행되었다. 회전속도는 1,500 r/min로 고정하였다. 수종은 낙엽송, 더글라스 퍼, 잣나무, 전나무, 느티나무이다. 실험결과 수종에 따른 적합한 삽입속도는 느티나무 75 cm/min, 낙엽송과 더글라스 퍼 100 cm/min, 전나무 150 cm/min, 잣나무 175 cm/min으로 나타났다. 하지만 모든 경우에서 연륜폭이 1 mm이하일 경우 연륜경계 확인이 어려운 것으로 확인되었다. 연륜폭이 1 mm이하인 경우를 제외하고는 연륜폭측정기와 레지스토그래피의 연륜폭그래프는 매우 일치하였다. 향후 연륜폭이 1mm 이하인 미세연륜 확인이 가능한 레지스토그래피가 개발된다면 레지스토그래피가 수령조사를 위해 전통적으로 활용되는 생장편의 연륜관찰방법을 대체할 수 있을 것이다. 또한 레지스토그래피의 연륜폭그래프는 생장량 조사에도 활용할 수 있을 것으로 판단된다.

1. 서 론

수목의 수령을 측정하는 대표적인 방법에는 연륜관찰법, 지절관찰법 및 직경측정법이 있다. 이들 방법 중 연륜관찰법이 수령을 추정하는 방법 중 가장 정확한 방법(Jeong et al., 2017; Seo et al., 2017a, b)임에도 불구하고 실제 활용된 사례는 드물다. 생장편 채취 시 발생되는 상처가 노거수의 생육에 피해를 유발하여 고사될 수 있다는 견해가 주요 요인이다. 하지만 수목은 상처가 생기면 수분증발 방지, 세균침입에 대한 자기방어(Shigo et al., 1977; Dujesiefken et al., 2006)뿐만 아니라, 상처 주위의 형성층과 유세포가 기계적, 화학적 특성이 정상세포와 다른 상해조직을 형성하여 상처를 덮기(Grunwald et al., 2002; Frankenstein et al., 2005) 때문에 생육에 큰 지장이 없다(Oh et al., 2017).

레지스토그래피는 바늘이 수목 내부에 들어가면서 목부의 밀도 차에 따른 전기저항의 차이를 그래프로 나타내어 수목의 내부 상태와 목재부재의 부후정도 등을 측정하는 장비로 개발되었다(Frank, 1994; Gruber, 2000). 국외에서는 주로 수목의 부후정도를 파악하는 용도로 이용되고 있으며(Fikret, et al., 2003; Denise, 2010; Frank, 2013), 고대 건물부재의 부후정도 확인(Ceraldi et al., 2001), 산불에 의한 상해조직(callus) 형성과 부후에 관한 분석(Michael et al., 2003), 산사태 영향에 의한 수목의 형태 분석(Saez et al., 2008) 등 다양한 분야에서 활용되고 있다. 국내에서는 레지스토그래피를 통해 목조문화재 및 목조시설물 부재의 평가가 가능한 것으로 확인(Lee et al., 2003; Hwang et al., 2008)되어 주로 목재 부재의 부후정도를 분석하는 비파괴진단의 용도로 활용되고 있다(Jung et al., 2014; Lee et al., 2014).

부후를 확인하는 것이 주요 목적인 레지스토그래피를 이용하여 수령을 조사한 연구는 드물다. 레지스토그래피는 현장에서 바로 조재와 만재의 구분을 그래프 상으로 볼 수 있는 장점이 있지만 조재와 만재를 구분하는 센서가 달린 부분이 약해 줄기가 단단한 수목이나 노거수 등의 수령을 측정하기에는 어려움이 따르기 때문이다(Son, 2007). 그러나 최근 레지스토그래피를 이용하여 연륜을 측정한 사례가 발표되었다. Bilgin et al.(2012)은 연륜이 뚜렷한 침엽수의 수령 측정에 레지스토그래피 활용이 가능한지 확인한 결과 P. brutia의 수령측정에 가능성이 있는 것으로 보고하였다. 수목의 흉고직경과 수령의 관계를 회귀식으로 만들어 수령을 추정한 후, 그 결과를 레지스토그래피를 이용한 수령 추정과 비교한 연구도 있는데, 이 연구에서도 레지스토그래 피의 유용성이 확인되었다(Lukaszkiewicz et al., 2005). 반면 국내에는 레지스토그래피를 이용한 수령 조사가 진행된 바가 거의 없는 실정이다. 따라서 본 연구에서는 연륜경계가 뚜렷한 수종들에 대해 레지스토그래피로 측정 검토하여 레지스토그래피 를 이용한 수령추정 가능성을 검토하는 것이 연구의 목적이다.

2. 재료 및 방법

2.1. 재료

레지스토그래피로 수령 조사를 위해 연륜경계가 뚜렷한 다섯 수종(Larix kaempferi, Pseudotsuga menziesii, Pinus koraiensis, Abies holophylla, Zelkova serrata)의 원판을 준비하였다(Table 1).

2.2. 방법

2.2.1. 레지스토그래피 회전 및 삽입속도

레지스토그래피(Fig. 1)의 측정용 바늘이 삽입되는 방향으로 정렬되어 있는 연륜을 연륜측정기(Lintab system)와 레지스토그 래피를 이용하여 각각 측정하였다. 레지스토그래피로 나이테 분석을 위한 그래프의 진폭은 40~60% 범위에 존재하는 것이 안정적이고 연륜경계가 뚜렷하다(IML Australia ⓒ, 2013). 레지스토그래피의 회전 및 삽입속도는 만재율을 기준으로 안정적인 진폭을 보일 때를 회전 및 삽입속도로 하였다.

2.2.2. 연륜측정기 및 레지스토그래피 연륜폭 비교

레지스토그래피로 작성된 그래프의 연륜폭을 수치화 하였다(PD-tool pro, Fig. 2). 수치화된 연륜폭은 원판에서 연륜측정기로 측정한 연륜폭그래프와 비교를 통해 장비의 정확도를 확인하였다.

3. 결과 및 고찰

3.1. 레지스토그래피 회전 및 삽입속도

원판에서 연륜측정기로 연륜측정 결과 낙엽송 연륜개수 36개 평균만재율은 27.92%, 더글라스퍼 연륜개수 29개 평균만재 율 31.71%, 잣나무 연륜개수 36개 평균만재율 12.94%, 전나무 연륜개수 32개 평균만재율 14.53%, 활엽수인 느티나무는 연륜개수 63개 평균만재율은 76.15% 이었다(Table 2). 레지스토그래피를 이용하여 연륜측정시 분석을 위한 안정적인 진폭범 위는 40 ~ 60%범위에 존재하는 것이라고 보고하고 있다(IML Australia ⓒ, 2013). 이 범위의 회전 및 삽입속도를 조사하기 위해 수종마다 만재율을 기준으로 회전속도와 삽입속도를 다르게 하여 연륜에 대한 저항값을 측정하였다(Ukrainetz et al., 2010; Frank, 2012). 그 결과 회전속도는 수종에 관계없이 1500 r/min일 때 연륜경계가 뚜렷한 것으로 나타났다(Fig. 3). 삽입속도는 만재의 비율이 높은 느티나무(만재율: 75.07%)의 삽입속도가 75 cm/min로 가장 느리게 나타났고, 만재의 비율이 중간정도인 낙엽송(만재율: 27.92%)과 더글라스 퍼(만재율: 31.71%)의 삽입속도가 100 cm/min 정도, 만재의 비율이 낮은 잣나무(만재율: 12.94%)와 전나무(만재율: 14.53%)는 각각 150, 175 cm/min로 측정하여야 안정적인 진폭과 뚜렷한 연륜경계 를 확인할 수 있었다(Table 2.). Fig. 4는 침엽수 중의 전나무와 활엽수인 느티나무의 진폭을 나타낸 것으로 뚜렷한 연륜경계를 나타내고 있다.

3.2. 연륜측정기 및 레지스토그래피 연륜폭

Table 3은 원판 5개에 대해 연륜측정기와 레지스토그래피로 연륜폭을 측정한 것이다. 두 방법으로 측정한 평균연륜폭을 비교하면 낙엽송 0.03 mm, 더글라스 퍼 0.08 mm, 잣나무 0.01 mm 차이가 났으며, 전나무와 느티나무는 동일한 값을 나타냈다. Table 4는 원판 5개에 대해 연륜측정기와 레지스토그래피로 연륜수를 측정한 것으로 4개 차이가 나는 낙엽송을 제외하고 모두 동일한 연륜개수를 나타냈다.

5수종에 대해 연륜측정기그래프와 레지스토그래피그래프를 비교한 결과 느티나무를 제외하고 모두 유사한 패턴을 확인할 수 있었다. Fig. 5는 전나무에 대해 연륜측정기그래프와 레지스토그래피그래프를 비교한 것으로 거의 일치하는 것을 볼 수 있다. 느티나무의 경우에는 심재, 변재와 관계없이 미세연륜이 전체적으로 분포하였다. 특히, 6번째에서 29번째까지 연륜 의 평균 연륜폭이 0.15 mm이었다(Fig. 6). 낙엽송은 변재부분의 평균 연륜폭은 0.07 mm 으로 변재부분의 미세연륜에 의해 연륜의 개수가 차이가 나는 것을 확인 할 수 있었다(Fig. 7). 따라서 두 측정방법의 결과인 연륜 개수에 차이가 나는 것은 미세연륜 때문인 것으로 보이며(Eckstein et al. 1994) 레지스토그래피로는 미세연륜에 대한 정확한 측정이 어려운 것을 확인할 수 있었다.

통계학적으로 비교한 결과에서 t-값은 느티나무를 제외하고 모두 3.5 이상으로 통계적으로 유의한 값을 가졌다(Table 5). 느티나무의 경우 1 mm이하의 미세연륜으로 인해 정확한 연륜폭 측정이 불가능하여 t-값이 0.8로 다른 수종에 비해 낮게 나타났 다. 부호의 일치도를 확인하는 Glk값은 낙엽송 91%, 더글라스 퍼 82%, 잣나무 83%, 전나무 92%로 통계적으로 유의한 결과를 확인할 수 있었다(Table 6). 느티나무의 경우 크로스데이팅이 잘 맞지 않는 미세연륜 부분인 1~20번째 연륜을 제외하고 분석하 면 육안관찰법에서 높은 일치도를 보이며(Fig. 8) t-값 4.2(overlap period 42), Glk값 68%로 통계적으로도 유의성 있는 결과를 얻었다. 따라서 레지스토그래피를 이용한 수령측정은 연륜폭이 1 mm이상의 연륜이 뚜렷한 수종에서 활용 가능할 것으로 판단되며 레지스토그래프로 얻은 연륜폭그래프를 대표연륜연대기와 크로스데이팅을 통한 그래프분석을 통해 정확한 수령 측정 이 가능할 것으로 판단된다. 또한, 레지스토그래피의 연륜폭그래프는 생장량 조사에도 활용할 수 있을 것으로 판단된다.

4. 결 론

본 연구는 수목의 수령을 측정하는 방법으로 레지스토그래피를 활용하는데 있어서 수종별로 가장 적합한 회전속도와 삽입속 도를 찾기 위하여 수행되었다. 실험에는 연륜경계가 뚜렷한 낙엽송, 더글라스 퍼, 잣나무, 전나무, 느티나무를 이용하였다. 실험결과 회전속도는 수종에 관계없이 연륜경계가 뚜렷이 나타나는 1,500 r/min으로 나타났고, 연륜경계가 뚜렷한 바늘의 삽입속도는 느티나무 75 cm/min, 낙엽송과 더글라스 퍼 100 cm/min, 전나무 150 cm/min, 잣나무 175 cm/min으로 확인되었다. 연륜폭측정기와 레지스토그래피를 이용한 그래프는 유의한 수준에서 일치하였다. 하지만 모든 수종에서 연륜폭이 1 mm이하일 경우에는 연륜경계 확인이 어려운 것으로 확인되었다. 향후 연륜폭이 1mm 이하인 미세연륜 확인이 가능한 레지스토그래피가 개발된다면 레지스토그래피를 이용한 수령추정이 전통적으로 활용되는 생장편의 연륜관찰방법을 대체할 수 있을 것이라 판단된 다. 또한 레지스토그래피의 연륜폭그래프는 생장량 조사에도 활용할 수 있을 것으로 판단된다.

References

Bilgin G., Adnan G., Gokhan K. Is Resistograph an Appropriate Tool for the Annual Ring Measurement of Pinus brutia?. NDE for safety / Defektoskopie. 2012.

Ceralid C., Mormone V., Ermolli E.R. Resistographic Inspection of Ancient Structures for the Evaluation of Mechanical Characteristics. Materials and Structures. 2001; 34(235):59-63.

Denise J., Gregory M., Michael T., Marc N. The Measurement of Wood Decay in Landscape Trees. Arboriculture & Urban Forestry. 2010; 36(3):121-127.

Dujesiefken D., Liese W. In: Dujesiefken D., Kockerbeck P., editors. Die wundrektionen von bἅumen- CODIT Heute. Jahrbuch der Baumpflege 2006: 21-40. 2006 Braunschweig: Thalacker Medien. .

Eckstein D., Saϐ U. Bohrwiderstandsmessungen an Laubbäumen und ihre holzanatomische Interpretation. Holz als Rohund Werkstoff. 1994; 52:279-286.

Fikret I., Bailian L. Rapid Assessment of Wood Density of Live Trees Using the Resistograph for Selection in Tree Improvement Programs. Canadian Journal of Forest Research. 2003; 33:2426-2435.

Frank R. Resistographic Visualization of Treering Density Variations. 1994 In: International Conference on Tree Rings, Environment, and Humanity.

Frank R. Basics of Micro-resistance Drilling for Timber Inspection. Holztechnologie. 2012; 53(3):24-29.

Frank R. Detecting Fungal Decay in Palm Stems by Resistance Drilling. Florida arborist spring 2013. 2013

10.

Frankenstein C., Eckstein D., Schmitt U. The Onset of Cambium Activity - A Matter of Agreement?. Dendrochronologia. 2005; 23(1):57-62.

11.

Gruber F. Vergleichende Messergebnisse zur Identifizierung von Schadstellen im Fichtenholz (Picea abies L. Karst.) mit den Bohrmessgeäten Teredo, Resistograph 1410 und Impulshammer–Schallmesssystem. Allgemeine Forest und Jagdzeitung. 2000; p. 172

12.

Grunwald C., Stabile J., Waldman J., Gross R., Wirgin I. Population Genetics of Shortnose Sturgeon Acipenser Brevirostrum Based on Mitochondrial DNA Control Region Sequences. Molecular Ecology. 2002; 11(10):1885-1898.

13.

Hwang W.J., Kanetaka S., Sasaki T. Possibility of Deterioration Diagnosis for Wooden Structures using Resistograph. 2008; In: Journal of the Korean Wood Science and Technology Conference Proceedings p. 71-72.

14.

15.

Jeong H.M., Kim Y.J., Seo J.W. Relationships between vessel-lumen-area time series of Quercus spp. at Mt. Songni and corresponding climatic factors. Journal of the Korean Wood Science and Technology. 2017; 45(1):72-84.

16.

Jung S.Y., Seo M.S., Hong J.Y., Kim S.J., Jung A.M., Kim J.S. Study on the Discoloration Identified from the Column of Wooden house, Hyunchungsa (Shrine) - Focused on Influence of Microorganisms and Correlation with Strength. Journal of National Cultural Properties Research Institute. 2014; 47(4):58-73.

17.

Lee K.J. An introduction to forest science. 2014 Seoul, Korea: Hyangmunsa Press. .

18.

Lukaszkiewicz J., Kosmala M., Chrapka M., Borowski J. Determining the Age of Streetside Tilia cordata trees with a DBH-BASED Model. Journal of Arboriculture. 2005; 31(6):280-284.

19.

Michael S., Erin M., Joseph M., Richard G. Use and Calibration of the Resistograph for Analysis of Oak (Quercus sp.) Decay and Callus Formation Associated with Fire Scars. 2003University of Missouri, Department of Forestry. .

20.

Oh J.A., Seo J.W., Kim B.R. Establishing Local Master Ring-Width Chronologies and Their Utilization for Estimating The Age of Big Old Trees. Journal of the Korean Wood Science and Technology. 2017; 45(1):85-95.

21.

Saez J.L., Corona C., Berger F. Use of Resistograph for Dendrogeomorphological Analysis of Avalanche Impacts (massif de l’Oisans, France). Geophysical Research Abstracts. 2008; 10.

22.

Seo J.W., Choi E.B., Ju J.D., Shin C.S. The association of intra-annual cambial activities of Pinus koraiensis and Chamaecyparis pisifera in Mt. Worak with climatic factors. Journal of the Korean Wood Science and Technology. 2017a; 45(1):43-52.

23.

Seo J.W., Jeong H.M., Sano M., Choi E.B., Park J.H., Lee K.H., Kim Y.J., Park H.C. Establishing tree ring δ 18O chronologies for principle tree species (T. cuspidata, P. koraiensis, A. koreana, Q. mongolica) at subalpine zone in Mt. Jiri National Park and their correlations with the corresponding climate. Journal of the Korean Wood Science and Technology. 2017b; 45(5):661-670.

24.

Shigo A.L., Marx H.G. Compartmentalization of decay in trees. USDA Forest Service Agriculture imformation Bulletin. 1977; :405.

25.

Son Y.M. Age measurement of trees. 2007National Institute of Forest Science. .

26.

Ukrainetz N.K., O'Neill G.A. An Analysis of Sensitivities Contributing Measurement Error to Resistograph Values. Canadian Journal of Forest Research. 2010; 40:806-811.